Cite this lesson as: Sanchez, S., & Deutsch, C.V. (2022). Domain Delimitation with Radial Basis Functions. In J. L. Deutsch (Ed.), Geostatistics Lessons. Retrieved from http://www.geostatisticslessons.com/lessons/implicitrbf
Implicit Boundary Modeling with Radial Basis Functions
Sebastian Sanchez
University of Alberta
Clayton V. Deutsch
University of Alberta
May 16, 2022
Learning Objectives
- Review the importance of stationary domains
- Review the framework of radial basis functions (RBF)
- Compare RBF interpolation and dual kriging
Introduction
A critical task in geostatistical modeling is the delimitation of domain boundaries. This is performed to satisfy the decision of stationarity used in geostatistical workflows. These domains can be based on grade, lithology, alteration, mineralization, structure or a combination of these factors. Historically, a manual interpretation of the domain boundaries was considered based on the experience and knowledge of the geologist. There could be different interpretations in presence of widely spaced data (Silva & Deutsch, 2012) and these can be time-consuming and difficult to reproduce.
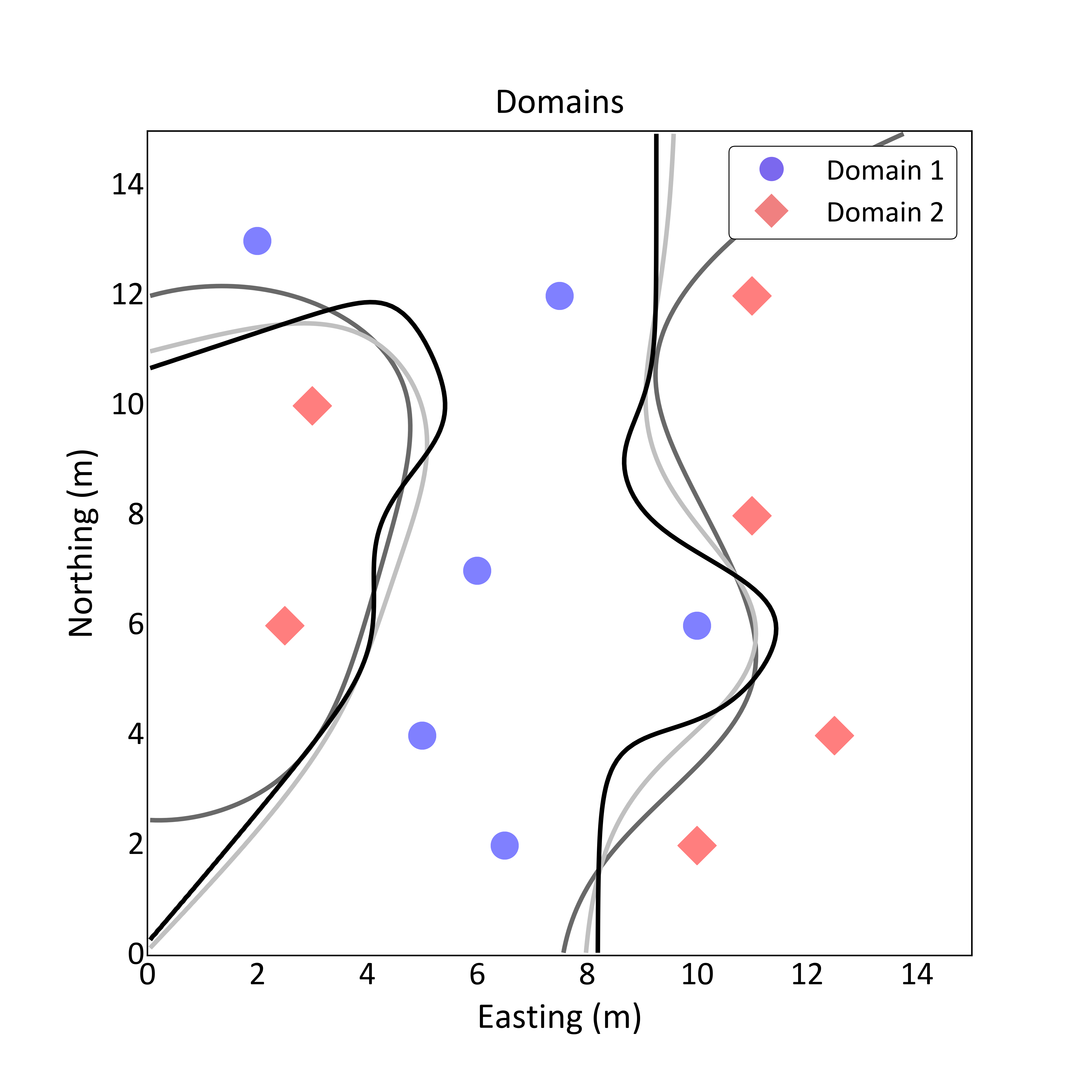
To supplement manual interpretation, several mathematical approaches have been developed for implicit modeling; a common method is the interpolation of signed distance functions using Radial Basis Functions (RBF) (Cowan et al., 2003). Signed distance functions have been widely used for implicit surface inference (Osher & Fedkiw, 2003). RBFs were first mentioned in the geological literature by (Hardy, 1971). The development of RBFs was in parallel to the work of Matheron on regionalized variables (Matheron, 1963). A key difference between RBFs and Kriging is that RBFs use a positive definite basis function and Kriging uses the covariance function for interpolation (Cowan et al., 2003). Additionally, Kriging often computes weights for each estimate using a local search neighborhood; RBFs conventionally use all samples to compute the weights once. There is a similar form of Kriging, called Dual Kriging (Chilès & Delfiner, 1999), that also computes the weights once. RBF and Kriging interpolation are discussed below.
For implicit boundary modeling, the distance between samples and the nearest sample of a different domain is calculated, negative values are set for samples that fall inside the domain being modeled and positive values for samples that fall outside. Then, the distances are interpolated and the boundary between domains is extracted where \(distance=0\). There are several methods for interpolation; discrete smooth interpolation (Mallet, 1989), classical geostatistical methods (Blanchin & Chilès, 1993) and RBF methods (Cowan et al., 2003), RBF with gradients and constraints (Hillier, Schetselaar, Kemp, & Perron, 2014) and RBF with local anisotropy (Martin & Boisvert, 2017). In this lesson, the Radial Basis Function (RBF) methodology will be reviewed. A comparison with Kriging will be presented.
Stationary Domains
Given a set of samples, two types of models can be used to predict values at unknown locations. If the laws that command the behavior of the samples are well known, a deterministic model can be inferred and the prediction of values is quite straightforward. Unfortunately, mineral deposits are typically the result of many complex and chaotic geological processes. These processes are too complex to define a deterministic model based on sparse data, thus, it is assumed that sample values are the result of stochastic processes. In these cases, a probabilistic model may be used (Isaaks & Srivastava, 1989).
In a probabilistic model, samples are considered to be realizations of random variables \(Z(\mathbf{u}_i)\) for \(i=1,...,N\). Several samples at each location \(\mathbf{u}\) would be needed to calculate probabilistic parameters such as the mean and variance. This is impossible since there is only one sample per location. To address this problem, the random variables \(Z(\mathbf{u}_i)\) are assumed to be stationary. Stationarity entails that the random variables follow the same probability laws independent of their location, therefore, probabilistic parameters, like the mean \(m(\mathbf{u})\), are the same at all locations. The assumption of stationarity is a key component in the derivation of geostatistical tools like Kriging (Isaaks & Srivastava, 1989).
The geologic region is divided into domains that are assumed to be stationary (McLennan, 2007). These domains are considered to be statistically homogeneous and share common geological characteristics. The definition of domains should lead to better reproduction of geological features and more reliable models.
Distance Functions
For clarity, the following assumes the presence of two domains; one that is inside and the other outside. The formalism can be extended to more than two domains. The first step is to assign an indicator to each sample. The indicator will take the value of \(1\) if the sample is inside the domain, or \(0\) if the sample is outside (Silva & Deutsch, 2012):
\[I(\mathbf{u}_i) = \bigg\{ \begin{aligned} &1 \;\;\;\;\text{ if $\mathbf{u}_i$ belongs to the domain} \\ &0 \;\;\;\;\text{ if $\mathbf{u}_i$ otherwise} \end{aligned}\] where, \(\mathbf{u}_i\), \(i=1,...,N\) are the locations of the samples. Then, the distance to the nearest sample with a different indicator is calculated:
\[DF(\mathbf{u}_i) = \bigg\{ \begin{aligned} &-argmin(r) \;\;\;\;\text{ if $I(\mathbf{u}_i)=1$} \\ &+argmin(r) \;\;\;\;\text{ if $I(\mathbf{u}_i)=0$} \end{aligned}\]where argmin() returns the minimum value and \(r\) is the Euclidean straight line distance:
\[r(\mathbf{u}_i,\mathbf{u}_j) = \sqrt{(x_i-x_j)^2+(y_i-y_j)^2+(z_i-z_j)^2}\] Commonly, geological domains have anisotropy, that is, a different length scale of continuity in different directions. In these cases, the distance between samples can be calculated by:
\[r(\mathbf{u}_i,\mathbf{u}_j) = \sqrt{\bigg(\frac{x_i-x_j}{ax}\bigg)^2+\bigg(\frac{y_i-y_j}{ay}\bigg)^2+\bigg(\frac{z_i-z_j}{az}\bigg)^2}\] where \(ax\), \(ay\), \(az\) are the ranges of anisotropy. The coordinates \(x\), \(y\) and \(z\) are rotated to align with the directions of principal continuity (Silva & Deutsch, 2012). These distance function values will be used as measurements for interpolation.
Radial Basis Function Framework
Given a set of measurements \(f(\mathbf{u}_i)\) at locations \(\mathbf{u}_i\), \(i=1,..., N\), an interpolator \(s(\mathbf{u})\) can be defined to predict values at any unsampled location. The interpolator should reproduce the measurements at their locations \(s(\mathbf{u}_i)=f(\mathbf{u}_i)\) (Fasshauer, 2007).
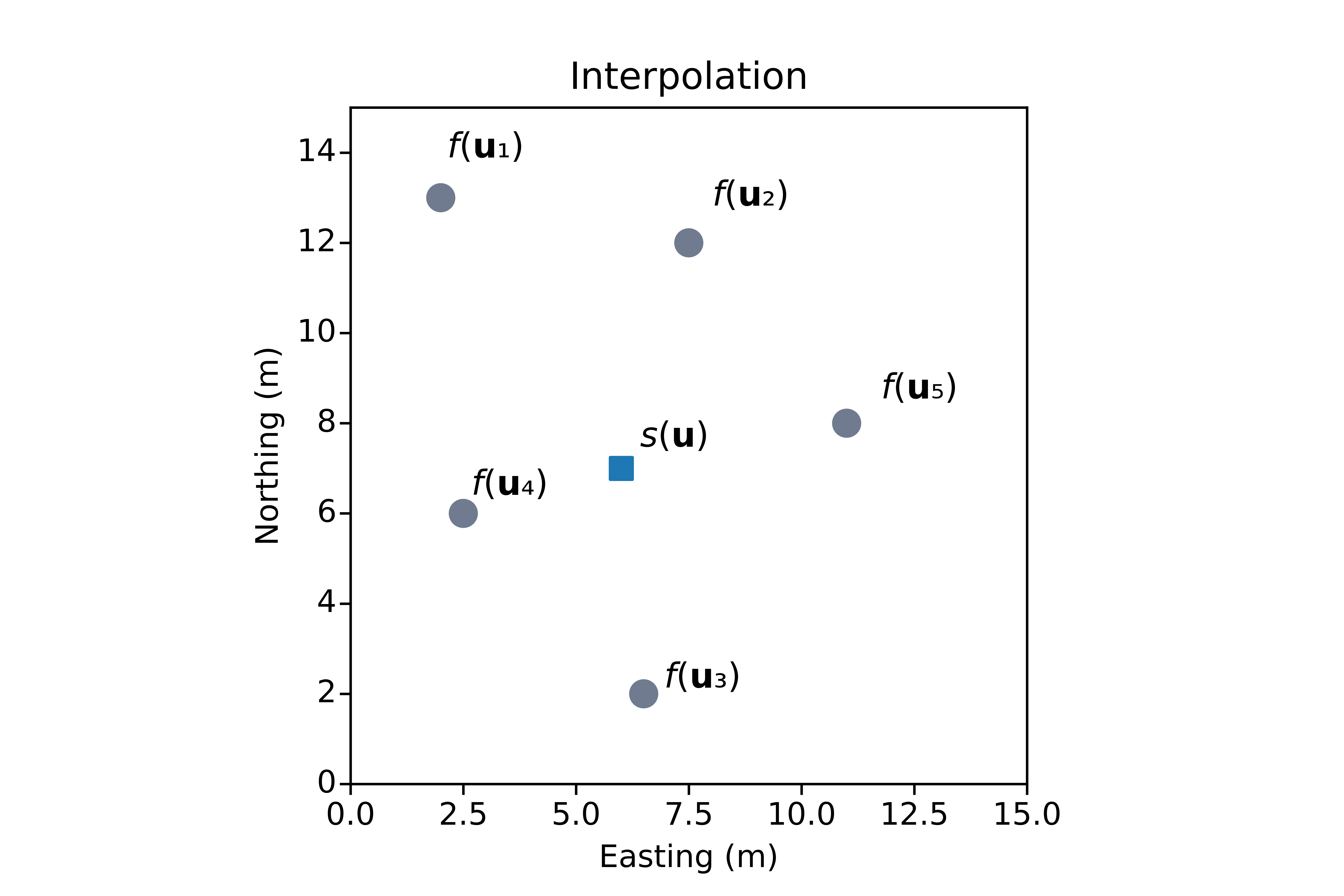
To define \(s(\mathbf{u})\), a common approach is to consider a weighted linear combination of functions \(B_i\) (Fasshauer, 2007):
\[s(\mathbf{u})=\sum_{i=1}^{N}w_i B_i(\mathbf{u})\]
The functions \(B_i\) are referred to as basis functions. The interpolator \(s(\mathbf{u}_i)\) has to replicate the measurements at their respective locations: \(s(\mathbf{u}_i)=f(\mathbf{u}_i)\), which leads to a system of linear equations:
\[\mathbf{A}w=f(\mathbf{u}_i)\]
\[\begin{bmatrix} B_1(\mathbf{u}_1) & B_2(\mathbf{u}_1) & \cdots & B_N(\mathbf{u}_1)\\ B_1(\mathbf{u}_2) & B_2(\mathbf{u}_2) & \cdots & B_N(\mathbf{u}_2)\\ \vdots & \vdots & \ddots & \vdots\\ B_1(\mathbf{u}_N) & B_2(\mathbf{u}_N) & \cdots & B_N(\mathbf{u}_N) \end{bmatrix} \begin{bmatrix} w_1\\ w_2\\ \vdots \\ w_N \end{bmatrix}= \begin{bmatrix} f(\mathbf{u}_1)\\ f(\mathbf{u}_2)\\ \vdots \\ f(\mathbf{u}_N) \end{bmatrix}\] where \(\mathbf{A}\) is a matrix of basis functions: \(A_{ij}=B_j(\mathbf{u}_i)\) for \(i,j=1,...,N\), \(f(\mathbf{u}_i)\) is a column vector of measured values and \(w_i\) are the weights. A transform of the distance function \(\phi(r(\mathbf{u},\mathbf{u}_i))\) can be used as the basis function \(B_i(\mathbf{u})=\phi(r(\mathbf{u},\mathbf{u}_i))\):
\[s(\mathbf{u})=\sum_{i=1}^{N}w_i\phi(r(\mathbf{u},\mathbf{u}_i))\]
If we consider that \(\phi(r(\mathbf{u},\mathbf{u}_1))=\phi(r(\mathbf{u},\mathbf{u}_2))\) if \(r(\mathbf{u},\mathbf{u}_1)=r(\mathbf{u},\mathbf{u}_2)\), then \(\phi(r(\mathbf{u},\mathbf{u}_i))\) has the same value for fixed distances \(r\) to a center location \(\mathbf{u}\). This means that \(\phi\) is radially symmetric to \(\mathbf{u}\), and hence, is named a Radial Basis Function (RBF) (Fasshauer, 2007).
As mentioned, the weights are found by solving a system of linear equations. To assure that the system has a solution, the RBF matrix is required to be positive definite (Fasshauer, 2007). Some commonly used positive definite RBFs are shown in the table below:
| RBF | Equation | Properties |
|---|---|---|
| Gaussian | \(\phi(r)=e^{-\epsilon^2r^2}\) | Positive definite |
| Spherical | \(\phi(r)=1.5\epsilon r-0.5(\epsilon r)^3\) | Positive definite, for r<1 |
| Exponential | \(\phi(r)=e^{-3 r/\epsilon}\) | Positive definite |
| Multiquadratic | \(\phi(r)=\sqrt{1+(\epsilon r)^2}\) | Conditionally positive definite |
| Linear | \(\phi(r)=r\) | Conditionally positive definite only in 1-D, parameter free |
Table 1: Selected radial basis functions (Fasshauer, 2007)
Where \(\epsilon\) is a chosen parameter. Kriging is perhaps the most broadly used interpolator in geostatistics, see next.
Ordinary Kriging
Ordinary Kriging (OK) is a widely used linear estimator:
\[z^{*}(\mathbf{u})=\sum_{i=1}^{N}\lambda_i \cdot z(\mathbf{u}_i)\] where \(z^{*}(\mathbf{u})\) is the estimated value at the unsampled location \(\mathbf{u}\), \(\lambda_i\) are weights and \(z(\mathbf{u}_i)\) are samples at locations \(\mathbf{u}_i\). The OK estimator constrains the estimator to be unbiased. To satisfy this constraint of unbiasedness, the sum of the weights has to be one (Isaaks & Srivastava, 1989). The weights are calculated by minimizing the error variance. The partial derivatives of the error variance and the constraint of unbiasedness provide \(n+1\) equations for \(n\) unknown weights and a Lagrange multiplier (Isaaks & Srivastava, 1989):
\[\sum_{j=1}^{N}\lambda_jCov(\mathbf{u}_i,\mathbf{u}_j) + \mu = Cov(\mathbf{u},\mathbf{u}_i) \,\,\,\, \forall i=1,...,N\] \[\sum_{i=1}^{N}\lambda_i=1\] where \(Cov(\mathbf{u}_i,\mathbf{u}_j)\) is the covariance between locations \(\mathbf{u}_i\) and \(\mathbf{u}_j\). The solution to this problem can be written as:
\[\mathbf{C}\lambda=c\]
\[\begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1N} & 1\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ C_{N1} & C_{N2} & \cdots & C_{NN} & 1 \\ 1 & 1 & \cdots & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \lambda_1\\ \vdots \\ \lambda_N\\ \mu \end{bmatrix}= \begin{bmatrix} c_1\\ \vdots \\ c_N\\ 1 \end{bmatrix}\] where, \(C_{ij}=Cov(\mathbf{u}_i,\mathbf{u}_j)\) and \(c_{i}=Cov(\mathbf{u},\mathbf{u}_i)\). The covariance between all pairs of locations is obtained from the variogram model. Usually, OK uses search neighborhoods for computational efficiency but, in the case of distance functions, all samples could be considered to reduce artifacts (Silva & Deutsch, 2012).
Dual Kriging
The equation for the kriging weights (see above) can be written as:
\[\lambda^{T}= c^{T}\mathbf{C}^{-1}\] Inserting these weights into the equation for the estimator leads to:
\[z^{*}(\mathbf{u})=c^{T}\mathbf{C}^{-1}z\] The product \(\mathbf{C}^{-1}z\) can be expressed as:
\[d=\mathbf{C}^{-1}z \,\,\,\, \,\,\,\, \,\,\,\,\] \[\mathbf{C}d=z \,\,\,\, \,\,\,\, \,\,\,\,\]
\[\begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1N} & 1\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ C_{N1} & C_{N2} & \cdots & C_{NN} & 1 \\ 1 & 1 & \cdots & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} d_1\\ \vdots \\ d_N \\ b\\ \end{bmatrix}= \begin{bmatrix} z(\mathbf{u}_1)\\ \vdots \\ z(\mathbf{u}_N)\\ 0 \end{bmatrix}\] where \(d=[d_1, d_2, . . ., d_N, b]\) is the result of the product \(\mathbf{C}^{-1}z\).
Then, the estimator can be written in the dual form as:
\[z^{*}(\mathbf{u})=c^{T}d\]
\[z^{*}(\mathbf{u})=\sum_{i=1}^{N}d_iCov(\mathbf{u},\mathbf{u}_i) + b\]
This is called the Dual Kriging form (Chilès & Delfiner, 1999). Dual Kriging is more computationally efficient than the primal form of Kriging because the weights \((d_i)\) are calculated just once for all estimates (Stewart, Lacey, Hodkiewicz, & Lane, 2014). The estimates are calculated by the weighted linear combination of covariances between the estimate location and the samples. Notice that Dual Kriging has a similar form to RBF interpolation, where:
\[\phi(r(\mathbf{u},\mathbf{u}_1))=Cov(\mathbf{u},\mathbf{u}_i)\] The covariance function can be considered as a radial basis function and the weights are calculated by a similar linear system of equations.
Example of RBF Interpolation
A boundary limit will be calculated from four samples from two different domains. The distance between samples and the nearest sample from other domain is calculated. By convention, negative distance values are assigned to samples of the domain been modeled:
| Sample | Domain | x | y |
|---|---|---|---|
| \(\mathbf{u}_1\) | 1 | 5 | 4 |
| \(\mathbf{u}_2\) | 1 | 10 | 6 |
| \(\mathbf{u}_3\) | 2 | 3 | 10 |
| \(\mathbf{u}_4\) | 2 | 11 | 8 |
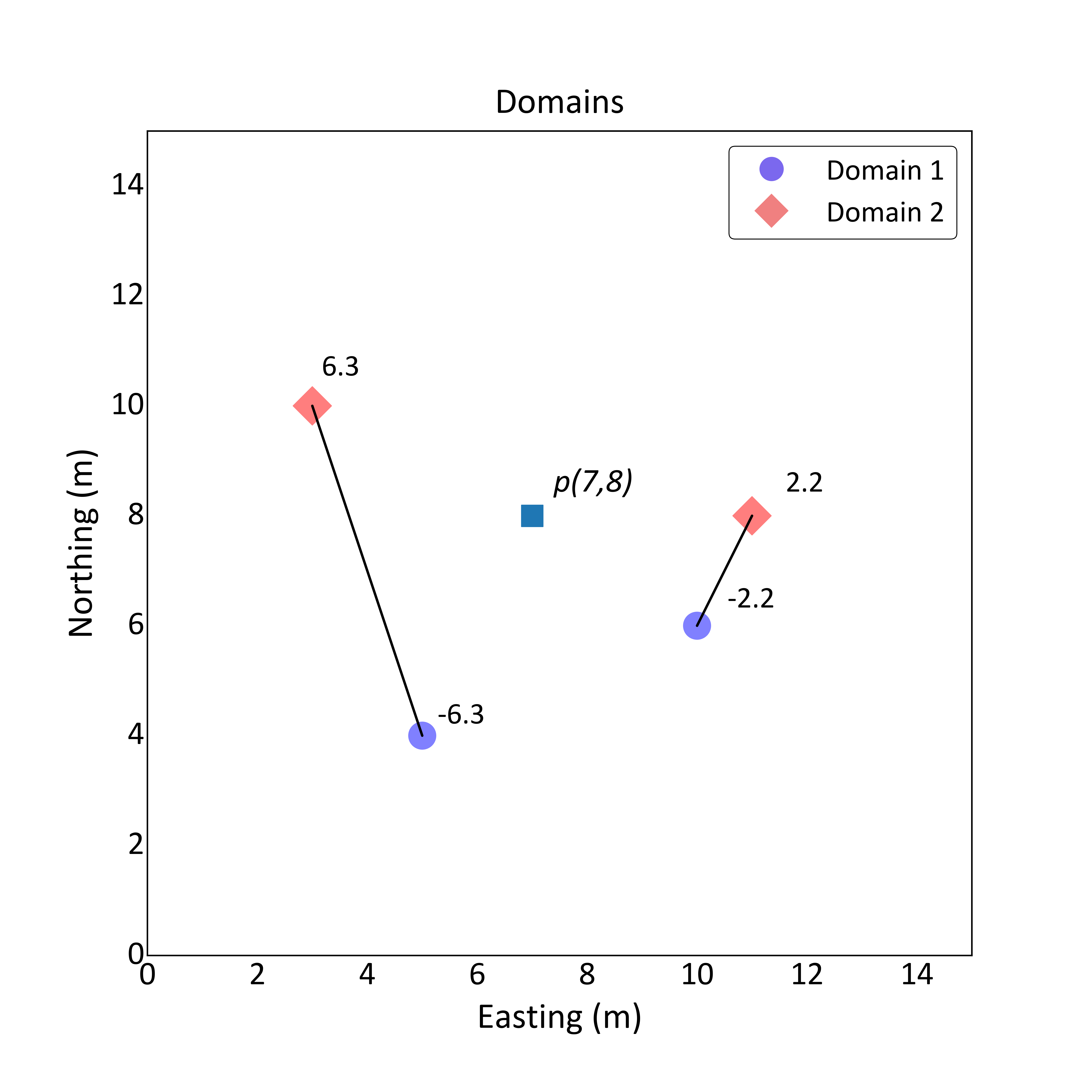
As an example, the interpolated distance at location \(p=(7,8)\) is calculated using the Gaussian RBF \(\phi(r)=e^{-\epsilon^2r^2}\) with \(\epsilon = 0.1\). The following equation is used to compute the weights:
\[\begin{bmatrix} \phi(r(\mathbf{u}_1,\mathbf{u}_1)) & \phi(r(\mathbf{u}_1,\mathbf{u}_2)) & \phi(r(\mathbf{u}_1,\mathbf{u}_3)) & \phi(r(\mathbf{u}_1,\mathbf{u}_4))\\ \phi(r(\mathbf{u}_2,\mathbf{u}_1)) & \phi(r(\mathbf{u}_2,\mathbf{u}_2)) & \phi(r(\mathbf{u}_2,\mathbf{u}_3)) & \phi(r(\mathbf{u}_2,\mathbf{u}_4))\\ \phi(r(\mathbf{u}_3,\mathbf{u}_1)) & \phi(r(\mathbf{u}_3,\mathbf{u}_2)) & \phi(r(\mathbf{u}_3,\mathbf{u}_3)) & \phi(r(\mathbf{u}_3,\mathbf{u}_4))\\ \phi(r(\mathbf{u}_4,\mathbf{u}_1)) & \phi(r(\mathbf{u}_4,\mathbf{u}_2)) & \phi(r(\mathbf{u}_4,\mathbf{u}_3)) & \phi(r(\mathbf{u}_4,\mathbf{u}_4)) \end{bmatrix} \begin{bmatrix} w_1\\ w_2\\ w_3 \\ w_4 \end{bmatrix}= \begin{bmatrix} f(\mathbf{u}_1)\\ f(\mathbf{u}_2)\\ f(\mathbf{u}_3)\\ f(\mathbf{u}_4) \end{bmatrix} \,\,\,\, \]
\[\begin{bmatrix} 1 & 0.75 & 0.67 & 0.59 \\ 0.75 & 1 & 0.52 & 0.95 \\ 0.67 & 0.52 & 1 & 0.51 \\ 0.59 & 0.95 & 0.51 & 1 \end{bmatrix} \begin{bmatrix} w_1\\ w_2\\ w_3 \\ w_4 \end{bmatrix}= \begin{bmatrix} -6.3\\ -2.2\\ 6.3\\ 2.2 \end{bmatrix} \,\,\,\, \]
Solving the system of equations gives:
\[\begin{bmatrix} w_1\\ w_2\\ w_3 \\ w_4 \end{bmatrix}= \begin{bmatrix} -12.2 \\ -27.8 \\ 14.5 \\ 28.5 \end{bmatrix} \,\,\,\, \]
The interpolated distance:
\[s(u)=\sum_{i=1}^{N}w_i\phi(r(\mathbf{u},\mathbf{u}_i))\] \[-12.2*0.82 + -27.8*0.88 + 14.5*0.82 +28.5*0.85= 1.65\]
As the weights do not depend on the location being estimated, interpolated distances can be computed at all locations. An example of RBF interpolation on a grid using the Gaussian RBF for different values of \(\epsilon\) is shown in the figure below (web version only). A boundary line is drawn where \(distance=0\):
An example of RBF interpolation on a grid using the Gaussian RBF for different parameters.
The RBF interpolation of signed distance functions is not constrained to a 2 dimensional grid only. It can be applied on a 3 dimensional grid and also be used for boundary delimitation of more than two domains:
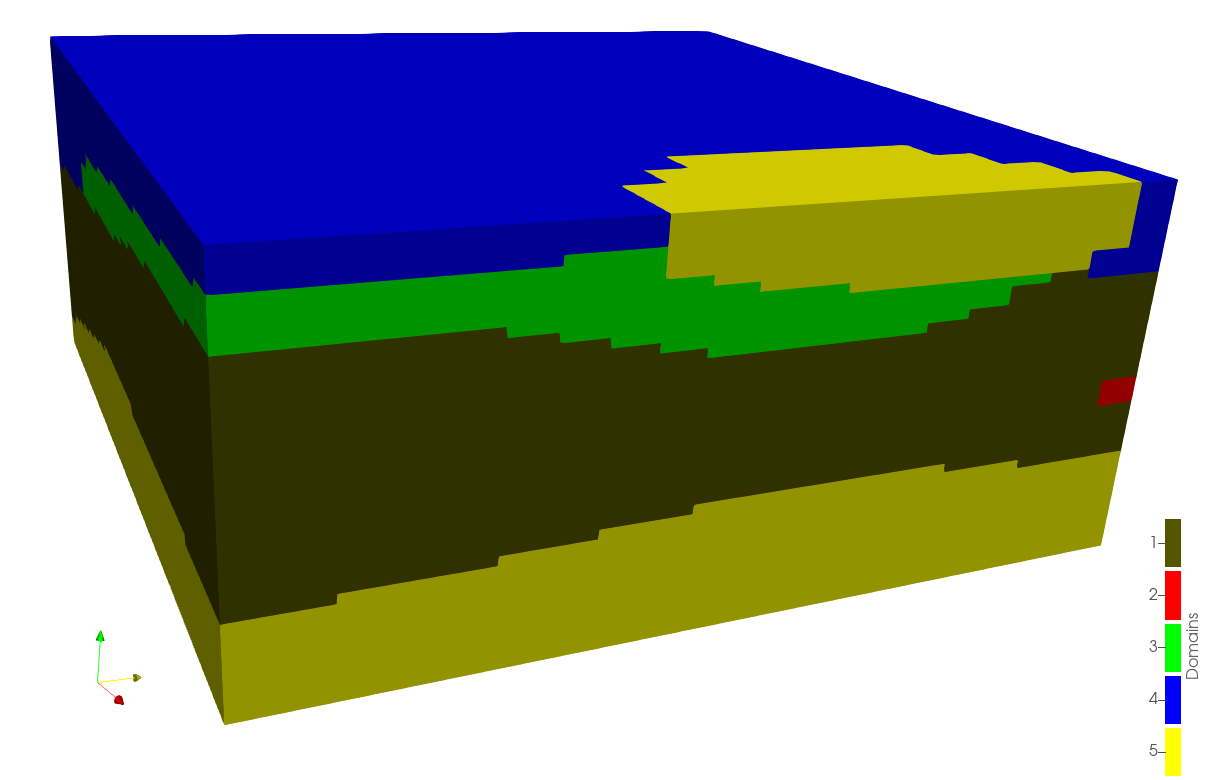
The extension to account for more than two domains will be reviewed below.
RBF and Kriging Comparison
Stationarity is assumed to derive the Kriging formulation. The measurements should satisfy this assumption to get reliable estimates. This constraint is challenging when interpolating distance due to the non-stationary nature of distance functions. In addition, Kriging methods use the variogram to obtain the weights. In some cases, the variograms are difficult to model and are not reliable (sparse sampling). As the RBF formulation does not rely on the assumption of stationarity and does not depend on variograms, it may be more robust in this situation (Cowan et al., 2003), although, estimates will be more accurate if stationarity is reasonably satisfied (Stewart et al., 2014).
Kriging aims to minimize and error or estimation variance. The minimized estimation variance can be computed and used as a measure of local estimation error that represents the data configuration (Rossi & Deutsch, 2013). There is no quantification of estimation variance in the RBF or Dual Kriging framework.
The variogram model is a way of describing the spatial correlation of the samples. Typically, the variogram is modeled using nested structures with different shapes and anisotropy (Rossi & Deutsch, 2013). Kriging uses covariance values obtained from the variogram model to optimally weight the samples. Certain RBFs can play a similar role in interpolation. The Gaussian and Inverse Multiquadratic functions are examples of this characteristic, where the parameter \(\epsilon\) determines the maximum influence distance of samples. As the functions used to model variograms are positive definite, they can also be used for RBF interpolation.
The example below shows implicit boundary modeling for three different RBFs with similar \(\epsilon\) parameter compared with Ordinary Kriging Dual form. There is a noticeable difference between the shapes of the boundary limits generated by the RBFs and Dual Kriging. The Gaussian RBF tends to generate a smooth boundary, whereas the others RBFs and Dual Kriging follow the shape of the samples. In the case of the Exponential RBF, RBF values approach zero faster than the Gaussian and Spherical RBFs values, producing a smaller boundary. The volume and shape of the boundary can be modify by changing the \(\epsilon\) parameter, as it represents the radius of influence of the samples. The shapes of the boundaries are fairly similar close to the samples, but they depart considerably in scattered areas. Consequently, The boundary shape will depend on the type of RBF used for interpolation, the \(\epsilon\) parameter, and the data spacing. The uncertainty of the boundary shapes could be calculated but RBFs and Dual Kriging do not deliver an uncertainty estimation. Although Ordinary Kriging Dual form is using a Spherical RBF as covariance function (with the same \(\epsilon\) parameter used for the Spherical RBF interpolation), it generates a closed boundary. Depending on the \(\epsilon\) value, the data may not influence unsampled locations that are far away. In the case of Dual Kriging, the component \(b\) in the estimator is an estimate of the global mean. When locations are far away, the summation goes to 0 and the \(b\) value prevails. In this example \(b\) has a positive value, limiting the extension of the boundary. The Simple Kriging Dual form is more similar to the RBF formulation as it does not have the \(b\) component.
RBF interpolation and Dual Kriging appear more computationally efficient than Kriging, but the size of the dataset must be reasonably small, say less than 10000. Larger systems require modifications, such as iterative solving methods (Beatson, Cherrie, & Mouat, 1999) or domain decomposition methods such as partition of unity (Martin & Boisvert, 2015).
Discussion
Even though RBF interpolation of distance functions is an established methodology for implicit modeling, it has some drawbacks that must be taken into consideration. Depending on the kernel used, RBF interpolation tends to be less reliable in sparse data areas and could generate biased extrapolation volumes at the edges of the model (Silva, 2015). Also, adding new data can change boundary limits a large distance away from the new data in an apparently arbitrary manner. The boundary limits are dependent on the drill hole spacing; the RBF interpolation may not put the boundary limit fairly centered between samples of different categories. Moreover, it is difficult to modify the interpolation approach to account for geological trends. Finally, there is no direct uncertainty inference. There is ambiguity in the location of the boundary in presence of widely spaced data, but interpolation algorithms provide only one best estimate. Some of these problems have been addressed in the literature. A brief discussion of RBF extensions and other applications follows.
An RBF methodology with local anisotropy is presented by (Martin & Boisvert, 2015). To include local anisotropy in the RBF framework, additional components are added to the formulation:
\[s(\mathbf{u})=\sum_{i=1}^{N}w_i\phi(r(\mathbf{u},\mathbf{u}_i))+\sum_{j=N+1}^{M}\alpha_j\nabla\phi(r(\mathbf{u},\mathbf{u}_j))+\sum_{k=M+1}^{O}\beta_kt_k\nabla\phi(r(\mathbf{u},\mathbf{u}_k))\] where \(i=1, \ldots ,N\) are sample locations \(f(\mathbf{u}_i)\), \(j=N+1, \ldots , M\) are gradient locations with strike-dip data where the potential field of the scalar function is normal to the planar orientation, \(\nabla f(\mathbf{u}_i)=n_j\), and \(k=M+1, \ldots , O\) are tangent locations where \(t_k\) is a line tangent to the surface of interest, \(t_k * \nabla f(\mathbf{u}_i)=0\). In some situations the set of samples may have an underlying function that should be reproduced. In these cases, a polynomial component can be added to the formulation (Fasshauer, 2007):
\[\sum_{l=1}^{M}b_lp_l(\mathbf{u})\] where \(p_l(\mathbf{u})\) are polynomials and \(b_l\) are coefficients.
The formulation for boundary delimitation can be extended for multiple domains (Silva & Deutsch, 2012). Instead of assigning a single indicator, an indicator vector \(I_k\) of size \(K\), say the number of domains, is assigned to each sample. A sample belonging to the domain \(k\) will have a 1 in the \(k\)-th element of the vector and zero in the \(K\)-1 remaining elements. Similar to before, the distance function is calculated for each element of the vector. Then, the signed distance function of each \(k\) domain is interpolated using RBF or Kriging. The domain at each location is assigned by taking the minimum estimated signed distance function at that location. A deeper insight of this methodology can be reviewed in the geostatistic lesson Signed Distance Function Modeling with Multiple Categories.
Another method for implicit boundary modeling is the interpolation of indicators. The methodology is described in detail by (Mancell & Deutsch, 2020). A 1/0 indicator is interpolated and thresholded at a value that leads to an unbiased proportion inside the domain. A nearest neighbor model is used to determine the unbiased proportion. One advantage of this method is that it can provide a model of uncertainty by changing the threshold value. Optimistic and pessimistic boundary models can be created.
One of the major components of mineralization uncertainty is geological uncertainty. Implicit modeling only delivers a deterministic domain model; there are modifications to incorporate uncertainty (Munroe & Deutsch, 2008) and (Wilde & Deutsch, 2011).
Summary
RBFs and Kriging are interpolation methods of distance functions for implicit domain boundary delimitation. Their formulation is similar, with differences regarding the assumption of stationarity, error quantification, computational efficiency and parameter selection. In recent years, variants have been developed to include geological trends, anisotropy and uncertainty. Many software use these methods for implicit geological modeling. The geologic modeler will almost always have to intervene to ensure that the resulting models satisfy complex geological constraints that defy simple incorporation into implicit modeling.