Learning Objectives

• Understand the implicit modeling methodology for constructing geologic models of multiple rock types based on the estimation of signed distance functions
• Observe the benefits and limitations of the method
• Select key parameters and understand their influence on the resultant models

Introduction

Geologic models describe the extent, shape, and volume of multiple rock types in space. Rock types are classified based on their physical, chemical, and mineral properties. Classically, geologic models are built with manual interpretation and digitization of cross sections. This explicit modeling method is suitable for models used later in geostatistical analysis. In recent years, implicit modeling techniques have been used to assist in geologic interpretation and the construction of geologic models. These methods are based on implicit functions for demarcating boundaries of multiple rock types and offer a rapid alternative to manual methods due to the dual formalism of the interpolator.

The distance function methodology is an implicit modeling technique based on the interpolation of signed distance functions over a modeling domain (Hosseini, 2009; McLennan, 2007; McLennan & Deutsch, 2006). Signed distance functions measure the separation of rock types with respect to each other. Distances depend on the orientation, geologic shape and extension of the rock types. Positive and negative distances distinguish between outside and inside a domain, respectively. Interpolation methods including kriging could be used to estimate the signed distance function values at unsampled locations; then, a cutoff rule sets the boundaries between multiple rock types.

This lesson describes and provides practical insights into the signed distance function implicit modeling method for multiple rock types. The method is computationally efficient and straightforward to implement since it does not require heavy parameterization and is able to reproduce and transfer large scale geological features into numerical models. The goodness, robustness, and limitations of the method are also analyzed.

Distance Function Approach for Multiple Rock Type Modeling

The signed distance function methodology (Osher & Fedkiw, 2003) is an implicit modeling technique where the function is constructed by interpolating a distance measure based on the conditioning data. For each sample, the distance between itself and the nearest sample belonging to an opposite domain is computed and assigned. The interface that separates the regions in space is determined by the sign of the estimated signed values.

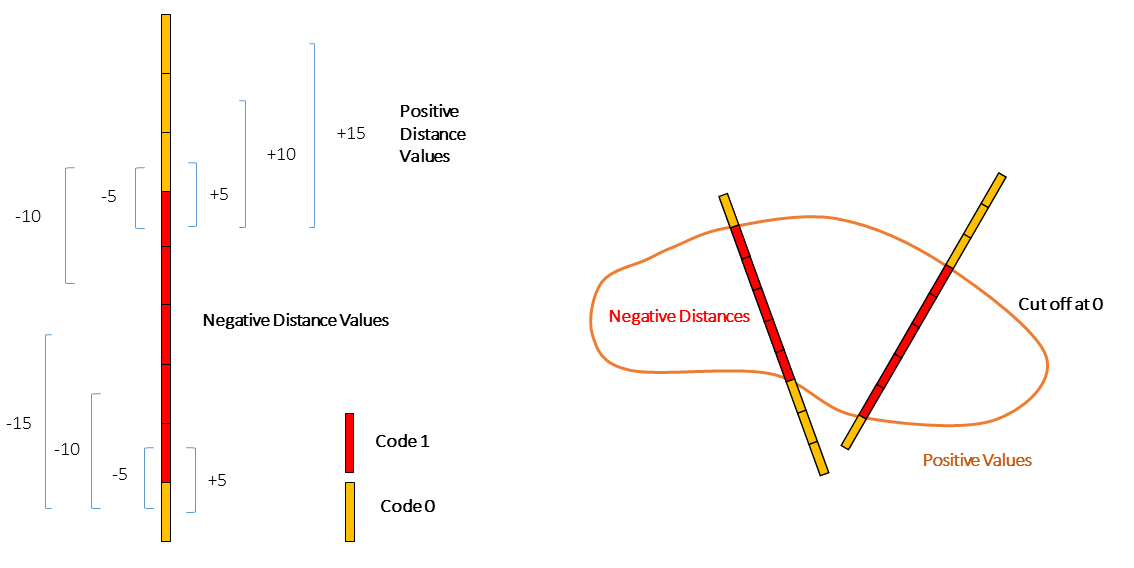
The Implicit Method for Multiple Rock Types

Consider \(K\) rock types in the deposit. For all sample locations \(\{z(\textbf{u}_\alpha), \alpha=1,\ldots,n\}\), an indicator vector of \(K\) elements is coded:

\[ i_k(\textbf{u}_\alpha) = \begin{cases} 1, & \mbox{if $z(\textbf{u}_\alpha)=k$} \\ 0, & \mbox{otherwise} \end{cases} \quad k=1,\ldots,K \]

This vector indicates the rock type associated with each sample. For a sample designated as rock type \(k\), the \(k\)-th element of the vector is one while the remaining \(K-1\) elements are zero. The signed distance value to the closest different domain is computed separately for each \(k\) element of the vector. By convention, if the sample is considered inside the domain, the distance is negative; otherwise, the distance is positive. The location \(\textbf{u}_\beta\) corresponds to the closest sample of a differing rock type to \(\textbf{u}_\alpha\). The Euclidean norm is used as the measure of distance:

\[ d_k(\textbf{u}_\alpha) = \begin{cases} -||\textbf{u}_\alpha - \textbf{u}_\beta||, & \mbox{if $i_k(\textbf{u}_\alpha)=1$} \\ +||\textbf{u}_\alpha - \textbf{u}_\beta||, & \mbox{if $i_k(\textbf{u}_\alpha)=0$} \end{cases} \quad k=1,\ldots,K \]

Given additional information on the anisotropy of the geologic features from exploratory data analysis, anisotropies could be incorporated for each rock type. No correlations among the distance values are considered.

The signed implicit function is then interpolated for all locations of interest. Kriging is preferred for this task due to its ability to account for directions of continuity and the spatial configuration of data. Other techniques such as inverse distance modeling could also be utilized. In particular, the use of global ordinary kriging is recommended due to its robustness and well-established practicality. This method does not search for data; using all the available data to estimate distance values at all locations avoids artifacts and shadows in the resulting models. The interpolation is performed individually for each rock type \(k=1,\ldots,K\). Ordinary kriging is applied multiple times:

\[ d_k^*(\textbf{u})=\displaystyle\sum_{\alpha=1}^n\lambda^{OK}_\alpha(\textbf{u})d_k(\textbf{u}_\alpha) \quad k=1,\ldots,K \]

When the multiple rock type variograms appear similar, a single variogram may be considered. This substantially reduces the processing time since the kriging equations are solved only once for all distance functions. After interpolating all \(K\) distances at the unsampled location \(\textbf{u}\), the rock type of the unsampled location is assigned:

\[ i^*(\textbf{u})=k' \quad \mbox{such that} \quad d_{k'}^*(\textbf{u})= \min\{d_k^*(\textbf{u})\}_{k=1}^K \]

The estimated distance provides a measure of proximity to the closest opposite domain. In this sense, the minimum estimated signed distance value may be seen as the most probable domain at an unsampled location.

Parameter Selection

Directions of continuity and preferred structural orientations of rock types must be accounted for when inferring the signed distance values and during the interpolation process. These directions and orientations may differ between rock types.

Variogram models and kriging estimation parameters will affect the final global proportions of each rock type in the model. This is important since there is some risk of introducing bias, affecting predictions of tonnage and grade. Special care is needed when selecting parameters for estimating the signed distance values; the resulting models must be visually validated and checked by the geomodeler.

Computation of Signed Distance Values

The Euclidean norm is used to calculate the distance between samples of multiple rock types; although other mathematical distances may be used, their implementation is neither justified nor advantageous. Depending on the type of deposit, anisotropy can be incorporated. Integrating anisotropy is required when modeling tabular or stratabound deposits where the horizontal spatial continuity is significantly different than the vertical direction.

Depending on the amount of data considered, the signed distance function methodology will provide interpretations that increase in complexity as data is increasingly collected. When dealing with scarce and widely spaced data, only linear relationships will be reproduced. When a large amount of data is available, the method can reproduce more complicated geometries since the drill holes have intersected more details of the deposit.

Signed Distance Variography

Variograms are inferred and modeled for each rock type separately. A detailed explanation of how to set up the parameters for the inference of experimental variograms may be found in (Deutsch & Journel, 1998 ) and other references. Preferential directions of continuity and the orientation of structural geological features must be accounted for in the signed distance variogram models. Due to non-stationarity of the distance values, these variograms may not have stationary sills. Also, the linearity of the distance measure makes the variogram values near the origin closely resemble a quadratic function. The Gaussian model is a well-suited structure for this type of very-continuous variogram. There should be no nugget effect in the variogram models of distance functions.

Variogram models influence the shape and spatial extension of the geologic domains. Changes in the spatial arrangements of multiple rock types may be linked to the variogram range parameters. Increasing the nugget effect tends to result in disconnected interpolated objects; a similar effect is observed when a short variogram range is used. Similarly, a low nugget effect, and long range continuous variogram models generate larger objects.

Kriging Parameters

The use of kriging is practically effective but theoretically questionable due to the strong non-stationary component of signed distance functions. The presence of trends may lead to edge issues and biased models when faced with sparse data. However, in practice, mineral estimation projects involve a considerable amount of data that, to certain extent, alleviates concerns about non-stationarity. Applying ordinary kriging typically results in satisfactory models from a practical point of view, as shown in the modeled porphyry deposit.

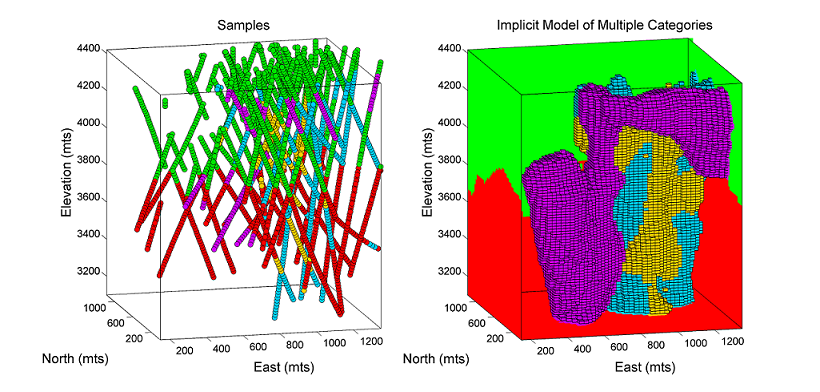
The main disadvantage of global kriging relates to the capacity to solve the large system of equations required. Global kriging is typically limited to approximately 10,000 samples. If there are more samples preventing the use of global kriging, a large search neighborhood is used. Using too few data in the kriging estimate will result in unrealistic edges and abrupt transitions between multiple rock types. The spatial configuration of samples is also important; the use of an octant search may also increase the reliability of kriged estimates when not using global kriging.

The Extrapolation Problem

A practical problem evident when applying the multiple signed distance function approach relates to the exaggerated presence of certain rock types at the edges of the model due to the extrapolation of signed distance estimates. There exist situations where the domains need to be constrained to control excessive extrapolation and to avoid the introduction of bias in the volumes of the resulting rock types. In particular, the spatial configuration of samples plays a large role in the extrapolation of distance estimates. Bias is visible in the following figures.

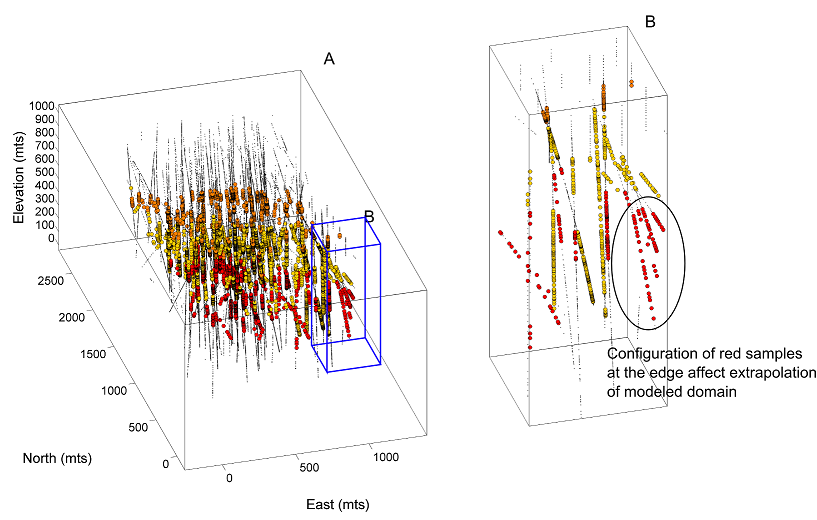
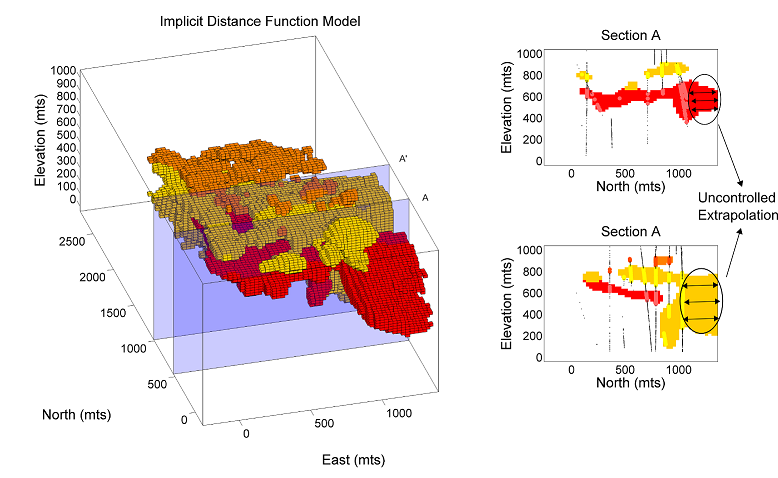
Extrapolation of rock types near the peripheral of the domain may be limited by artificially introducing samples at the edge of the models which conform to the geologic interpretation. The major disadvantage of this is that some geologic knowledge is necessary to constrain the additional data.

Another option consists of applying the distance function algorithm in a hierarchical fashion. Hierarchical rock type modeling may limit unreasonable extrapolation provided that there is a reasonable hierarchy in the defined rock types. Applying simple kriging in place of ordinary kriging and adjusting mean values may also be used to manage extrapolation. Each of these approaches requires care when applying them to manage extrapolation of rock types near boundaries. These changes add complexity to the approach and add another potential source of bias in the resulting models.

Summary

Signed distance function modeling is a powerful technique to aid in the geologic interpretation process. The use of an implicit function helps ensure a reasonable characterization of geological features if used properly. The method works with multiple rock types simultaneously, accounts for objectivity, reduces the time-consuming interpretative work, alleviates the workload when doing auditable revisions, and offers an easy manner to update models when new data becomes available. A variety of sensitivity analyses may be performed by modifying the parameters involved in the interpolation of the implicit function. The method avoids overlapping issues among domains; no priority criterion is needed. It is also straightforward to implement and is implemented in many geostatistical software packages.

Among the disadvantages, one may find that the interpolated domains surfaces are too smooth for the required model application. In addition, implicit models do not consider geologic controls including geologic trends and specific features that may lead to improved results if an explicit technique were used. The use of kriging only considers linear relations between samples; more complex geometries such as folded structures or curvilinear shapes call for other geostatistical techniques such as coordinate transformation or locally varying anisotropy. The non-stationarity behavior of the signed distance makes variogram inference challenging. Finally, there are often edge effects and uncertainty in the boundaries that is not accounted for.

References