Learning Objectives

• Understand the principle of merging secondary variables
• Review the calculation of super secondary variables with examples
• Appreciate the applications of secondary variable aggregation

Introduction

Secondary data, including seismic attributes, geological trends and previously modeled properties contain information to constrain modeling of additional variables. They are often available exhaustively and help with geostatistical prediction of primary variables available from drilling.

Some legacy software considers (1) only one secondary variable in collocated kriging, or (2) the difficult to model linear model of coregionalization. A practical solution is to aggregate multiple secondary variables into a single super secondary variable, allowing conventional cokriging, collocated cokriging and cosimulation to be used.

Almeida & Journel (1994) proposed joint simulation of multiple variable with a Markov-type coregionalization model. Babak & Deutsch (2009b) put forward the method of merging multiple secondary data and a variant of collocated cokriging using an intrinsic model avoiding variance inflation and other problems in the original formulation. Boisvert, Rossi, Ehrig, & Deutsch (2013) applied super secondary variables in Olympic Dam Mine Project to simplify response surface modeling and cosimulation.

Regarding the collocated correlation structure, ideally, the secondary data should have low correlation to each other and high correlation to the primary data. This would minimize redundancy and maximize predictive ability. There may be challenges with variables that are non-stationary, that is, the correlation coefficients may need to be changed locally. As another limitation, combining variables that have different spatial structure into a single super secondary variable will incur a loss of information. Cokriging techniques using the super secondary variable would provide for only secondary variable variogram. This lesson aims to provide some understanding about the use of super secondary variable.

Methodology

Prior to merging secondary variables, it is convenient for all the variables to be standardized or normal score transformed. We will also assume there are no missing data or a missing data management and imputation strategy has been implemented ahead of time.

Notation

Consider one location at a time, that is, we will not add the standard \(({\mathbf{u}})\) notation for location in this introduction. At each location, uppercase \(X_i,i=1,\ldots,n_{sec}\) are \(n_{sec}\) secondary variables and \(Y\) is the primary variable to be predicted, lowercase \(x_i,i=1,\ldots,n_{sec}\) and \(y\) represent the particular number for corresponding outcomes. All variables are standardized with mean of 0 and variance of 1. \(X_{ss,non}\) denotes the non-standardized super secondary variable and \(X_{ss}\) denotes the standardized super secondary variable, their outcomes are \(x_{ss,non}\) and \(x_{ss}\) separately. \(\rho_{ij},i,j=1, \ldots , n_{sec}\) are the correlation values between pairs of secondary variables. \(\rho_{iY} ,i=1,\ldots, n_{sec}\) are the correlation between each secondary variable and primary variable under consideration, \(\rho_{YX_{ss}}\) is the correlation coefficient of the super secondary variable with the primary variable. \(\mu_i,i=1,\ldots,n_{sec}\) are the weights for each secondary data.

Theory

The goal of the super secondary variable formalism is to build a function , \(x_{ss,non}=f(x_1,\ldots,x_{n_{sec}})\), to maximize correlation wth the primary variable, which can combine all the information in the \(n_{sec}\) secondary variables into a single super variable. For convenience, we standardize the \(X_{ss,non}\) to have a mean of 0 and variance of 1.

The super secondary variable \(X_{ss,non}\) at each location is a linear combination of the available secondary variables \(X_i,i=1,\ldots,n_{sec}\).

\[x_{ss,non}=\sum_{i=1}^{n_{sec}} \mu_i x_i\]

For getting maximum correlation between the super secondary variable and the primary variable, we need to minimize a mean squared error:

\[\text{max} \ E \{X_{ss,non} Y \} \equiv \text{min} \ E \{[X_{ss,non}-Y]^2 \}\]

The \(\ E \{[X_{ss,non}-Y]^2 \}\) is just the familiar cokriging error variance \(\sigma_{E}^{2}\) (Pyrcz & Deutsch, 2014). The cokriging error variance is expressed as:

\[ \sigma_{E}^{2} = \sum_{i=1}^{n_{sec}}\sum_{j=1}^{n_{sec}}\mu_i \mu_j \rho_{ij}-2\sum_{i=1}^{n_{sec}} \mu_i \rho_{iY} +1 = 1-\sum_{i=1}^{n_{sec}} \mu_i \rho_{iY} \]

The super secondary weights \(\mu_j,j=1,\ldots,n_{sec}\) can be calculated by the error variance in the same way with solving cokriging weights.

\[ \sum_{j=1}^{n_{sec}} \mu_j \rho_{ij} = \rho_{iY}, i=1,\ldots\,n_{sec}\]

The standard deviation of the nonstandard super secondary variable \(\sigma_{ss,non}\) is used to standardize the super secondary variable \(X_{ss,non}\) as below:

\[x_{ss}= \frac{x_{ss,non}}{\sigma_{ss,non}}\]

The variance of the non-standardized super secondary variable \(\sigma_{ss,non}^{2}\) can be found from the equation:

\[ \sigma_{ss,non}^{2}=1- \sigma_{E}^{2}=\sum_{i=1}^{n_{sec}} \mu_i \rho_{iY} \]

The correlation of the super secondary variable and the primary variable \(\rho_{YX_{ss}}\) is equal to the standard deviation of the super secondary variable \(\sigma_{ss,non}\).

\[\rho_{YX_{ss}}=E\{X_{ss}Y \}=\frac{\sum_{i=1}^{n_{sec}} \mu_i \rho_{iY}}{\sigma_{ss,non}}=\sigma_{ss,non} = \sqrt{\sum_{i=1}^{n_{sec}} \mu_i \rho_{iY}} \]

So the standardized super secondary variable \(X_{ss}\) is calculated as:

\[ x_{ss} = \frac{x_{ss,non}}{\sigma_{ss,non}} = \frac{\sum_{i=1}^{n_{sec}} \mu_i x_i}{\rho_{YX_{ss}}} \]

Brief summary

Consider \(Y({\mathbf{u}})\) is the primary variable to be simulated at location \(\mathbf{u}\) within a stationary domain \(\mathbf A\). There are \(n_{sec}\) secondary variables such as seismic attributes and previously simulated primary variables at the same location denoted as \(X_i({\mathbf{u}}),i=1,\ldots, n_{sec}\). The super secondary variable \(X_{ss}({\mathbf{u}})\) is defined as follows:

\[ x_{ss}({\mathbf{u}}) = \frac{\sum_{i=1}^{n_{sec}} \mu_i x_i ({\mathbf{u}})}{\rho_{Y X_{ss}}} \]

Where the \(\mu_i\) values are the weights to the secondary data, \(\rho_{Y X_{ss}}\) is the correlation coefficient between the merged secondary data and the primary data being estimated. The weights \(\mu_i\) are solved from the cokriging equations:

\[ \sum_{j=1}^{n_{sec}} \mu_j \rho_{ij} = \rho_{iY}, i=1,\ldots,n_{sec} \]

Where \(\rho_{ij}\) are the correlation coefficients between pairs of secondary variables, \(\rho_{iY}\) are the correlation between each secondary variable and the primary variable under consideration. The correlation coefficient of the super secondary variable and the primary variable is calculated as:

\[ \rho_{Y X_{ss}} = \sqrt{ \sum_{i=1}^{n_{sec}} \mu_i \rho_{iY} }\]

So we can apply the solved \(\mu_i\) and \(\rho_{Y X_{ss}}\) to calculate the aggregated variable \(x_{ss}({\mathbf{u}})\).

The aggregated super secondary variable contains all of the information contained in the \(n_{sec}\) secondary data relevant for the primary variable under consideration. The correlation of the primary to the aggregated variable is always positive and greater than the absolute value of any particular correlation of secondary variables to the primary. The weights and aggregated values would change if a different primary variable is considered. It is also interesting to note that the weights are the same at all locations since only collocated correlations are used. The weights and correlation of the aggregated variable to the primary would change if a subset of secondary variables is available.

Example

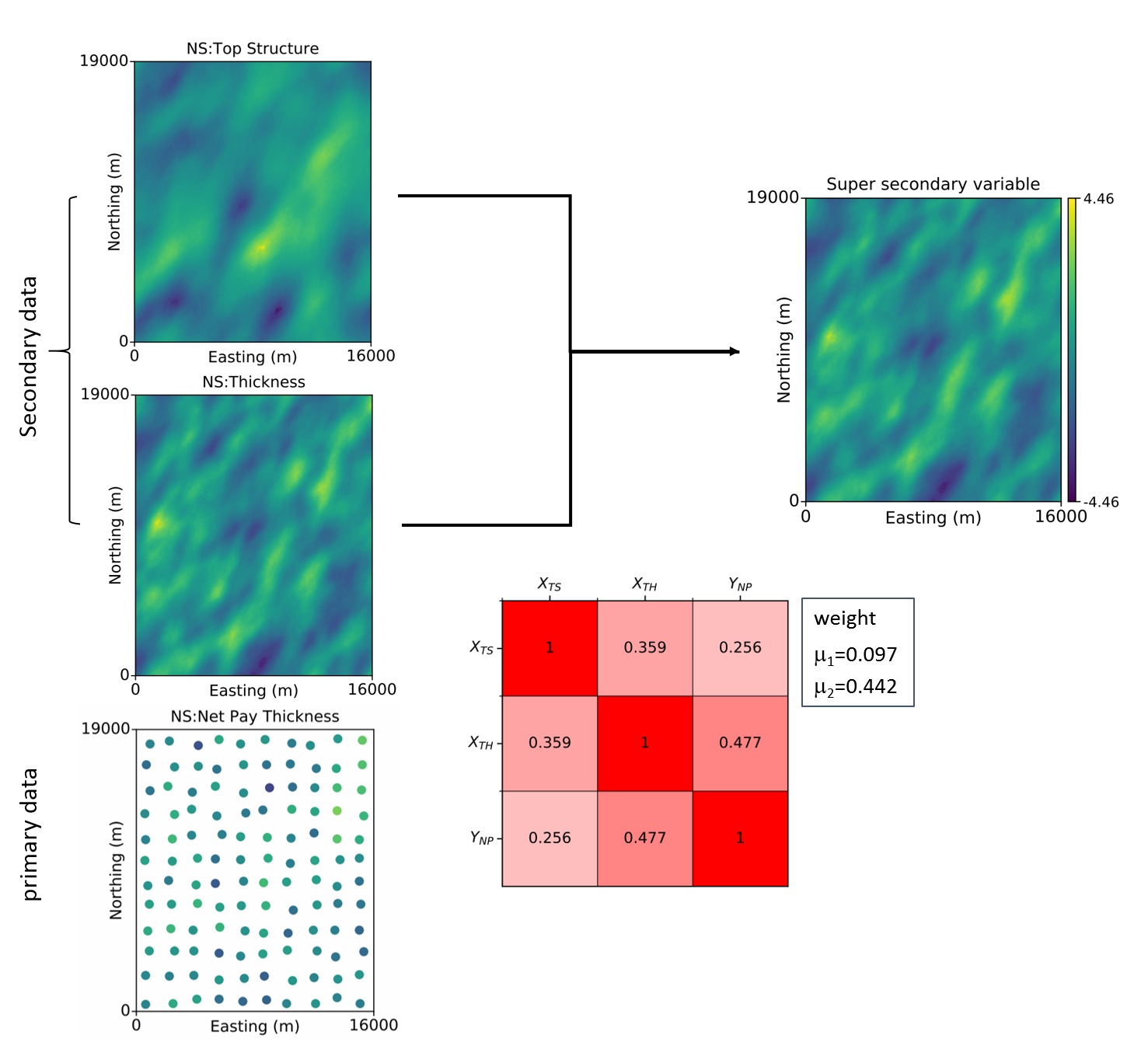
The following example is based on a normal score transformed geological data set. It has the primary variable of Net Pay Thickness (\(Y_{NP}\)) and two secondary data set of Top Structure (\(X_{TS}\)) and Thickness (\(X_{TH}\)). The secondary variables have a correlation coefficient of 0.359. Their correlations to the primary variable are 0.256 and 0.477, respectively. The system of equations to be solved is:

\[ \mu_1 + 0.359\cdot\mu_2=0.256 \]

\[ 0.359\cdot\mu_1 + \mu_2=0.477 \]

We can solve for the weights for each secondary variables: \(\mu_1\)=0.097 and \(\mu_2\)=0.442. The correlation coefficient of merged secondary data with the primary variable is:

\[ \rho_{Y X_{ss}} = \sqrt{\sum_{i=1}^{n_{sec}} \mu_i \rho_{iY}} = \sqrt{0.097\cdot0.256+0.442\cdot0.477} = 0.485 \]

Thus, the merged secondary variable is given by:

\[ x_{ss} = \frac {0.097\cdot x_{TS}+0.442\cdot x_{TH}}{0.485} \]

The following figure illustrates how this could be applied in practice. The two exhaustive grids of secondary data are shown to the upper left. The primary drill data are shown below them on the lower left. The correlation matrix and weights are illustrated in the middle. The weights are applied at each grid location and the aggregated super secondary variable is shown at the upper right.

Readers using a web browser may use the interactive figure which has 9 different cases that are divided into 3 groups, namely weak, medium and strong, based on the correlation of secondary variables to primary variable. For each group, we fix the correlation value of secondary variables to primary variable then gradually change the correlation between the secondary variables. The weights to the two secondary variables are displayed.

Use the slider at the bottom to view the different cases and weights calculated.

Application

There are many applications for super secondary variables. Constraining geostatistical models to all available data is important for the greatest prediction accuracy and precision.

Secondary data integration provides us with information to improve primary variable prediction. A combined super variable is treated as a new secondary variable for consideration in subsequent geostatistical modeling, which is a powerful and attractive method to simplify geostatistical simulation. There are various alternative methods for secondary integration, including collocated cokriging, Bayesian updating and stepwise conditional transform that work well for model construction, particularly when there is only one secondary variable (Pyrcz & Deutsch, 2014).

Super secondary variables can also be used in a hierarchical approach. A useful workflow (Babak & Deutsch, 2009a, 2009b) suitable for most modern software would be to (1) aggregate all available secondary data together for the prediction of the first primary, (2) simulate the first primary using the first super secondary considering intrinsic collocated cokriging (ICCK), (3) aggregate all available secondary data and the first primary for prediction of the second primary, (4) simulate the second primary using the latest super secondary and ICCK, and (5) repeat steps 3 and 4 using all available data.

Another application is to combine variables to reduce the number of variables going into response surface modeling or regression. An example of linear regression is shown in Boisvert et al. (2013). The model is built with four combined super secondary variables instead of more than one hundred original variables. The merged variables reduce the number of variables and lower the risk of over-fitting, which is helpful to accurately determine regression coefficients.

Conclusion

Merging secondary data accounts for how related the secondary are to the primary variable being predicted and also accounts for the redundancy between the secondary data. This approach is theoretically sound; the detailed process of derivation can be found in the paper (Babak & Deutsch, 2009a), it shows that using a single supersecondary variable in collocated cokriging produces the same result as using multiple secondary variable. The use of a single merged secondary variable greatly simplifies geostatistical modeling. This relative simplicity of simulating with only one secondary variable instead of many makes this technique attractive.

References