Learning Objectives

• Motivate the use of the Gaussian distribution
• Understand the mechanics of quantile-to-quantile transformation
• Review the requirement of a representative source distribution
• Understand transformation details including despiking and tail extrapolation

Why Do We Use the Gaussian Distribution?

Parametric models sometimes relate to an underlying theory, for example, the Gaussian distribution is the limit distribution for the sum of many independent random variables. Although some variables can be qualitatively described by similarities to parametric distributions such as the Gaussian (normal) or lognormal distribution, in practice, there is no general theory that would predict the form of probability distributions for earth science related variables.

Although the rock properties that we model are not Gaussian distributed, the multivariate Gaussian distribution is unique and permits the straightforward inference of conditional distributions; there are no practical alternatives to compute conditional distributions and simulate continuous properties. Modern geostatistical algorithms and software all invoke the multivariate Gaussian (MG) distribution for probabilistic prediction of continuous properties. A requirement of the MG distribution is that the univariate distribution must be Gaussian. The procedure developed early on in multivariate statistics and adopted by geostatistics is to: (1) transform the data to a univariate Gaussian distribution, (2) proceed with algorithms that take advantage of the properties of the multivariate Gaussian distribution, then (3) back transform results to original units.

The simplicity of the multivariate Gaussian distribution arises from its compact parametric form: it is fully parameterized by a mean vector and a variance-covariance matrix.

\[ f_{Y}(y_1,y_2,\ldots,y_n) = \frac{1}{\sqrt{(2\pi)^{n} |\Sigma| }} exp \left(-\frac{1}{2}(\mathbf{y}-\mu)^{T} \Sigma^{-1} (\mathbf{y}-\mu) \right) \]

where \(\mu\) is a column vector of means, \(\mu_{Y_1}, \mu_{Y_2},\ldots,\mu_{Y_n}\), \(\Sigma\) is a symmetric variance-covariance matrix between all pairs of \(n\) random variables or locations and \(|\Sigma|\) is the determinant of \(\Sigma\). Geostatisticians typically assume the mean and variance are stationary and calculate the covariance values from the variogram. The decision of stationarity is made for a geologic domain where the assumption of constant mean, variance, and variogram is reasonable. Perhaps the most important property of the multivariate Gaussian distribution is that all conditional distributions are Gaussian in shape and parameterized by mean and variance values arising from the normal or simple cokriging equations.

So, the transform of continuous property data to a Gaussian distribution is commonplace in geostatistics. Conditional distributions and multiple realizations are calculated in Gaussian units and the results are back transformed. The mechanics of the quantile-to-quantile normal scores transform are presented first, then we discuss workflow steps and implementation details.

Quantile-to-Quantile Normal Scores Transformation

The standard normal distribution is the target distribution: \[f_Y(y) = \frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}y^2}\] where \(f_Y(y)\) is the standard normal probability density function. There is no closed form analytical solution to the cumulative standard normal distribution, represented by \(F_Y(y)\), but there are excellent polynomial approximations (Kennedy, 1980).

The quantile-to-quantile normal score transformation matches the \(p\)-quantile of the data distribution to the \(p\)-quantile of the standard normal distribution. Consider the data variable \(z\) with the cumulative distribution function \(F_Z(z)\). This will be transformed to a \(y\), normal score value with standard normal the cumulative distribution function \(F_Y(y)\) as follows: \[y = F_Y^{-1}(F_Z(z)) \;\; \forall \; z\]

The \(nscore\) program in GSLIB implements this (Deutsch & Journel, 1998). A graphical representation of this procedure, shown below, is useful to understand the normal score transformation. The histograms are shown at the top of the figure. The cumulative distributions, shown at the bottom, are used for transformation. To transform any core porosity (say 10.0): (1) read the cumulative frequency corresponding to the porosity, and (2) go to the same cumulative frequency on the standard normal distribution and read the normal score value (-0.45). Any porosity value can be transformed to a normal scores value in this way.

Readers using a web browser may use the following interactive figure which shows the transformation from an original distribution to the Gaussian distribution by quantile.

Normal score transformation from an original porosity distribution to the Gaussian distribution. Use the slider at the bottom to manipulate the porosity value transformed.

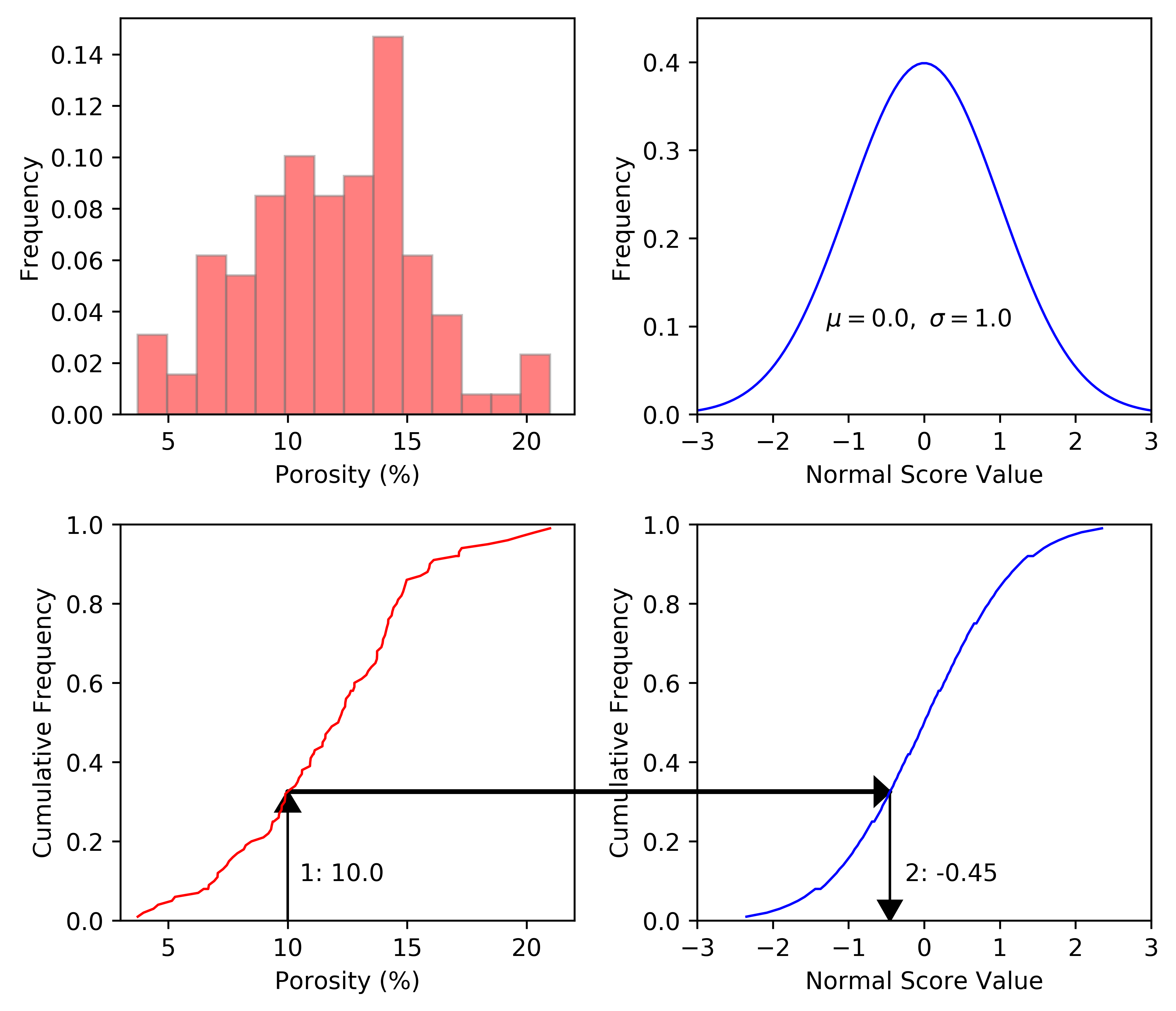
The transformation to a Gaussian distribution is straightforward; however, there are a number of implementation details to consider including the need for a representative distribution.

Representative Source Distribution

A representative distribution, \(F_Z(z)\), is required for each variable within each chosen stationary domain. These distributions may be of a residual after removal of a trend model. Any errors in the source distribution, such as bias, missing ranges, and spikes will be propagated through the modeling workflow. The representative source distribution must be modeled.

Typically the representative source distribution is a non-parametric distribution represented as a list of data values with declustering weights. Cell declustering is reviewed in a lesson. If distribution smoothing or fitting has been applied then the data values are replaced by values representing the fitted distribution. The non-parametric distribution is constructed by sorting the values in ascending order such that, \(z_1 < z_2 < \ldots < z_n\). The weights assigned to each data are carried with the data in the sorting process. The cumulative probabilities are calculated \(cp_i=\sum_1^i w_i\) and then averaged with the value below (with \(cp_0=0.0\)) to avoid a systematic bias due to the less than or equal to definition of the cumulative distribution function.

Modern workflows integrate uncertainty through multiple realizations of the source distribution, \(F^{\ell}_{Z(z)}, \forall \; \ell = 1,\ldots,L\). Each realization may be the result of a stochastic process such as spatial bootstrap or expert inferred scenarios.

Distribution Despiking

Multiple values that are at the same numerical values are called spikes. These values often occur at analytical detection limits, such as the minimum or maximum detection values on an assay. The Gaussian distribution has no spikes and these values must be ordered prior to transformation. This ordering procedure is called despiking. Despiking can be important for data with values at or below detection limit and are typically represented by a significant fraction of \(0.0\) values in the dataset. This is common with geochemical data in exploration and less common in Mining and Petroleum applications. Completely random despiking introduces artificial variability. Ordering the values by a moving average of the data avoids this problem, but introduces artificial continuity. A blended approach is increasingly used where the ties are broken partly based on a moving average and partly with a random component.

Isolating the spike of zero values into a separate population is recommended if possible. If the values of the spike are mixed with the other values of the population, then despiking must be considered. Random despiking may be acceptable if there are a very small percentage of values at the spike. The idea of using local moving averages for despiking was proposed by Verly (Verly, 1984). The idea is to compute averages within local neighborhoods centered at each tied data value. The data are then ordered or despiked according to the local averages; high local averages rank higher. As mentioned above, this transformation may introduce too much continuity. A blended approach where some randomness is added to the moving averages has shown promise.

Back Transformation

A back transformation is applied after a Gaussian-based algorithm has calculated all conditional distributions and simulated realizations within the stationary domain. This is the reverse of the forward transform: \[z = F_{Z}^{-1}(F_Y(y)) \;\; \forall \; y\] On the previous figure, one could imagine reversing the black arrows, that is, starting at 2 and going back to 1.

The back transformation is sensitive to the tails of the distribution. The data minimum and maximum are unlikely to represent the ultimate minimum and maximum of the property for the entire stationary domain. The practitioner is suggested to choose reasonable minimum and maximum tail values and rely on a simple extrapolation function. In GSLIB, linear, hyperbolic and power tail extrapolation models are available (Deutsch & Journel, 1998), but the linear one is simplest.

Special Topics

The transformation should take place prior to variogram analysis. The variogram of the Gaussian transform is required to parameterize the required covariances. The Gaussian transform removes outliers and smooths other irregularities in the distribution that lead to noisy experimental variograms (Pyrcz & Deutsch, 2014).

Gaussian simulation methods may be applied on latent variable(s) as in the case truncated Gaussian and pluriGaussian simulation. There are additional considerations for modeling univariate and multivariate Gaussian distributions, formulation of the truncation mask, data coding and transformation (Armstrong et al., 2011). Transforming inherently categorical variables to continuous data values must be done considering spatial correlation and considering non uniqueness of the results.

There are times when fitting the quantile-to-quantile transformation results with Hermite polynomials is convenient, for example, in change of support. The Hermite fit is also used in disjunctive kriging (Ortiz, Oz, & Deutsch, 2003).

References