Learning Objectives

• Understand stratigraphic coordinate transformation calculations
• Recognize when stratigraphic coordinate transformations should be applied
• Evaluate when different correlation grids should be applied
• Assess the impact of stratigraphic coordinate transformation on spatial models

Introduction

Geostatistical modeling requires understanding the spatial continuity of variables, ideally, this spatial continuity correctly considers geological features and represents a consistent domain. When these features are linear and do not change within the modeling domain, a Cartesian coordinate system is appropriate and distances can be calculated along a straight line path between points i.e., the shortest distance between two points is a straight line (Descartes, 1965). However, the use of a Cartesian coordinate system and Euclidean distances in geostatistical modeling is not appropriate for complex geology containing non-linear features due to faulting, folding, and other deformations; continuity in these types of deposits is often considered to follow along the geology. In these cases, one method is to transform the domain to an alternative coordinate system to support geostatistical techniques that rely on linear two-point pairings, such as kriging or sequential Gaussian simulation (SGS) that use variograms to characterize spatial continuity. One other approach is to use locally varying anisotropy and related methods in domains that exhibit non-linear features (Boisvert, Manchuk, & Deutsch, 2009).

Multiple coordinate transformations exist, the focus here is stratigraphic coordinate transformation. The purpose of stratigraphic coordinate transformation is to alter the coordinates in a way that removes the distortive effects of non-linear features and captures the original geological continuity of the formation when it was deposited (i.e., layers). Performing simulation or estimation in these alternative coordinate systems usually leads to better results because distances and spatial continuity are more consistent with geology. It must be noted that the methods discussed here are not limited to stratigraphic formations and other geological formations such as veins or high-angle mineralized breccias can also benefit from these transformations [Caumon & Mallet (2006)](Mallet, 2002).

The focus of this lesson is to explain the coordinate transformation process, highlight when different transformations are appropriate for different geological settings, and discuss the geostatistical modeling implications of these coordinate transformations.

When to Apply Stratigraphic Coordinate Transformation

Stratigraphic formations are layered deposits consisting of multiple strata of sedimentary rock, soil, or igneous rocks that are laid in parallel by natural processes. Upon deposition, layers are often horizontally extensive with a smaller vertical dimension. The original continuity of these layers can be altered by folding and faulting, which results in the distorted layers present today. Modeling the non-linear spatial continuity along these layers is important for boundary modeling and subsurface property modeling including petrophysical properties, facies, rock types, and mineral grades in stratigraphic deposits.

The distortion of the original strata can be reversed by modeling the bounding surfaces and correcting the coordinates of samples and grids within the strata. This correction results in a space where modeling with linear geostatistical techniques (e.g., SGS, kriging) is appropriate. This coordinate transformation is appropriate and necessary for all distorted, but otherwise flat, formations including veins that are extensive in one plane.

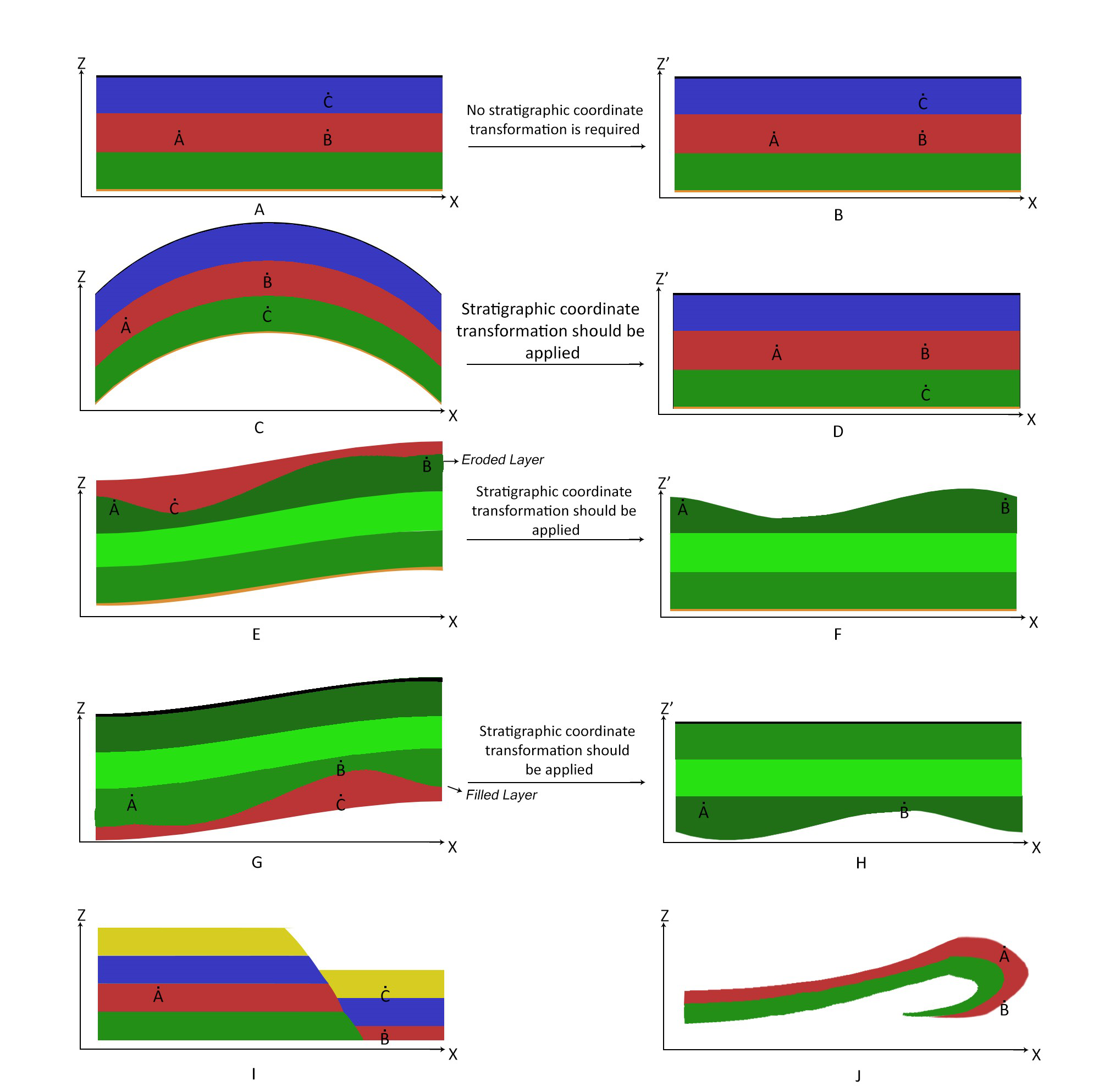
Examples of situations where stratigraphic transformation is appropriate are shown in the figure below. Here, points A and B belong to the same stratum, but C does not. The first formation (A) does not require a coordinate transformation, the relationship between points is linear, and traditional geostatistical modeling workflows can be applied directly (B). The second formation (C) has been folded since deposition and requires a coordinate transformation to flatten (D). Here, both bounding surfaces have remained intact and are flattened. The third example (E) shows folding and subsequent erosion of lower layers (green), followed by deposition (red). In this example, the green layers must be transformed separately; but this flattening can only consider the lower surface, as the top surface that would control this feature has been lost to erosion (F). G is an example of a formation that has been filled from below, but the top bounding surface is intact. Here, the green layers are transformed by flattening to the top surface. I is an example of a faulted formation that cannot be transformed to its original shape using stratigraphic coordinate transformation. J shows a layer folded back on itself and is inappropriate for stratigraphic coordinate transformation. However, example J can be first processed with an unfolding transformation and the recumbent folds can then apply a stratigraphic transformation.

Transformation Procedure

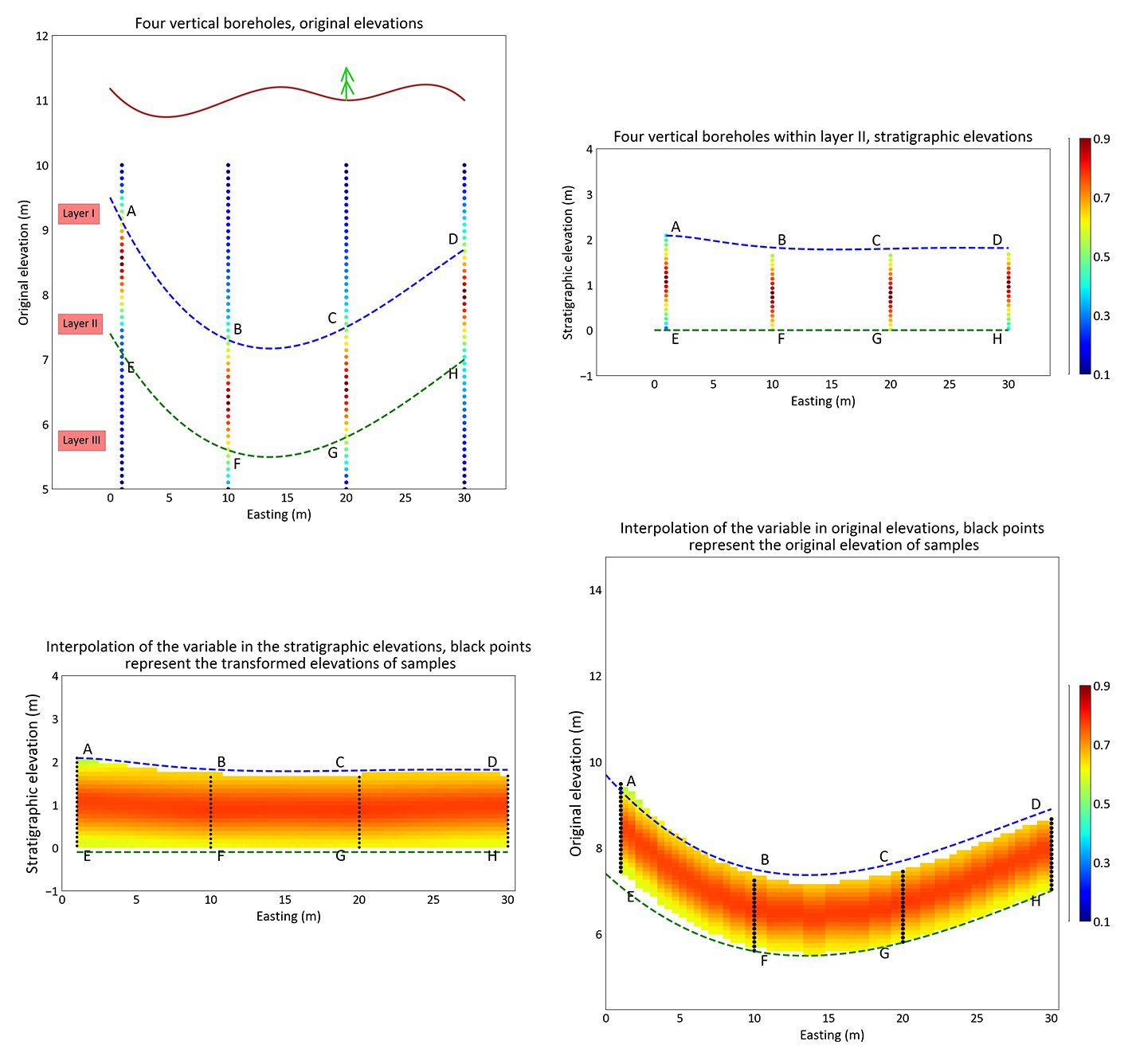
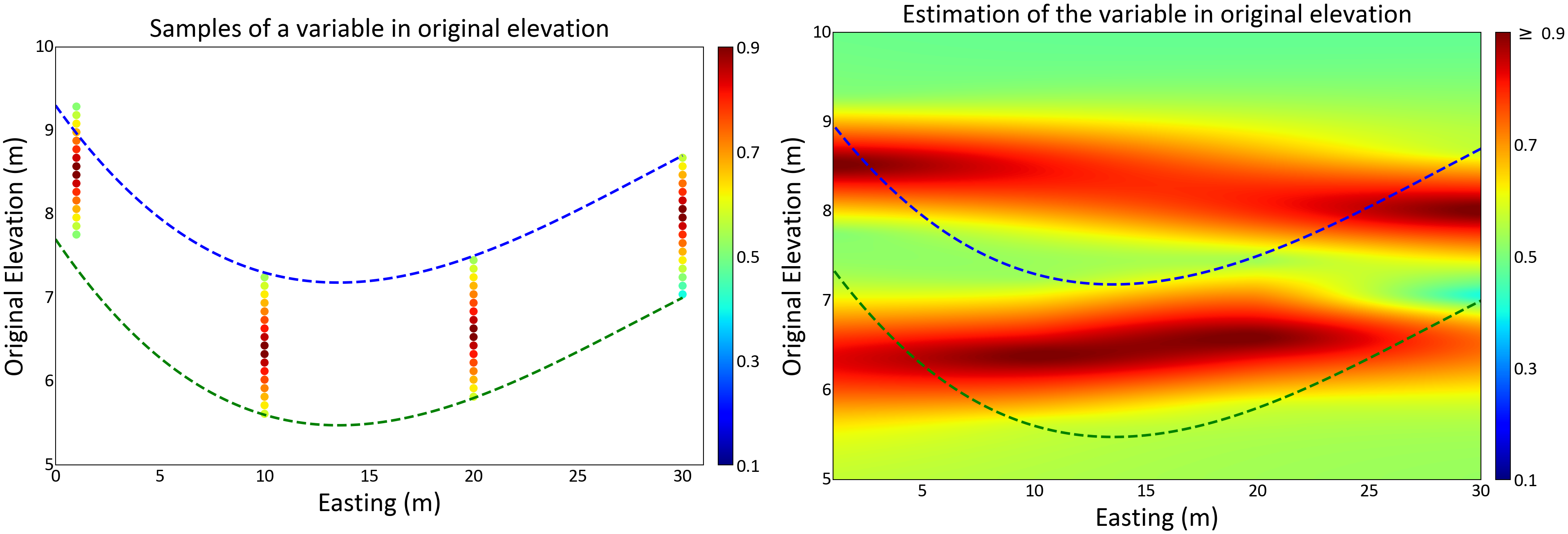
The original coordinates (X, Y, Z) are transformed into stratigraphic coordinates (X, Y, Z’). Geostatistical modeling is performed using the new stratigraphic coordinates and the modeling grid is back-transformed to the original coordinates (X, Y, Z). The first following figure demonstrates the process of modeling in stratigraphic coordinates. The continuity of the variable of interest follows along the surfaces determined by the geologist. However, if stratigraphic coordinate transformation was not considered, continuity imposed on the model would be unrealistic and not follow the geology, as shown in the second figure below.

Forward Transformation

The bounding surfaces of a layer might have been eroded, filled, or remained intact since deposition. The original continuity can be restored by modifying the elevation of points and flattening to the intact layers using bounding surfaces; if one layer has been eroded, only one bounding surface is considered. These intact layers are considered to be correlational surfaces and they define the correlation grid. There are four different transformations depending on the nature of the top and bottom surface, proportional, truncation, onlap, and combination (Pyrcz & Deutsch, 2014).

1- Proportional: top and bottom surfaces are intact and both surfaces are used to transform elevations. The new elevation of each point is its relative position between the top and bottom surface. This can be thought of as the proportion of the distance into the layer where this point exists. The transformation equation and an interactive example are shown below:

\[Z_{rel}=\frac{Z-Z_{cb}}{Z_{ct}-Z_{cb}} * T\]

The calculation to obtain the transformed elevation \(Z_{rel}\), requires the current elevation of the point \(Z\), and the elevation of the bottom and top surfaces \(Z_{cb}\) \(Z_{ct}\). \(T\) is the average thickness of the layer which standardizes the units of the transformed space, if this is ignored (i.e., set to 1.0), the resulting coordinate system describes the proportion of the distance into the layer.

An interactive illustration of a stratigraphic formation with proportional transformation style. Left: samples from four boreholes in original elevations. Right: stratigraphic transformation of the samples based on the definition of the top and bottom surfaces. The bottom slider changes the elevation of point A and results in a different flattening of the samples.

2- Truncation: the top surface has been eroded but the bottom surface is intact, only the bottom surface is used to transform elevations. Points are flattened to the bottom surface and represent the distance from the bottom correlational surface. The transformation equation and an interactive example are shown below:

\[Z_{rel}= Z - Z_{cb}\]

An interactive illustration of a stratigraphic formation with truncation transformation style.

3- Onlap: used to represent filling and the bottom surface has been shifted in a way that cannot be corrected. The top surface is intact and is used to transform elevations. Points are flattened to the top surface and represent the distance from the top correlational surface. The transformation equation and an interactive example are shown below:

\[Z_{rel}= Z - Z_{ct}\]

An interactive illustration of a stratigraphic formation with onlap transformation style.

4- Combination: used to describe a layer that has been both eroded and filled, as a result, both the top and bottom surfaces have been altered in a way that cannot be corrected. No correlational surface can be explicitly defined so the stratigraphic coordinate transformation is not possible.

Back Transformation

After coordinate transformation and modeling in the stratigraphic coordinate system, each grid cell in the model must be back-transformed to the original coordinates. The surfaces used for transformation must be exhaustive in the modeling domain to permit back-transformation of the grid between boreholes. The back-transformation formulas for each transformation style are:

1- Proportional:

\[Z= Z_{cb} + \frac{Z_{rel}}{T} * (Z_{ct} – Z_{cb})\]

2- Truncation:

\[Z = Z_{rel} + Z_{cb}\]

3- Onlap:

\[Z = Z_{rel} + Z_{ct}\]

To reiterate, geostatistical modeling techniques often rely on two-point statistics where the correlation between points is required to be linear (a.k.a. along a straight line); spatial continuity is modeled with variograms, and then used in Kriging and SGS workflows. When correlation is `along a surface’ rather than described by a straight line, modeling accuracy is improved when implemented on stratigraphic coordinates because spatial continuity is more consistent with the deposition of the feature of interest. These equations for transformation and back-transformation are used to create a space where the correlation between points mimics the original depositional environment and is along a straight line.

Modelling Considerations

Choosing the transformation style

Selecting which transformation is appropriate is typically based on a geological understanding of that layer (Pyrcz & Deutsch, 2014); this can be used to determine which layers are intact and appropriate for flattening. If there is no geological understanding available to determine correlational surfaces, different transforms can be tested and the one that results in the most continuous horizontal variogram can be inferred to be the best style to represent that layer (Mclennan, 2004). When several layers are present in a stratigraphic formation, each layer must be modeled independently with a transformation style that is appropriate for that layer.

Support and Volume Distortion

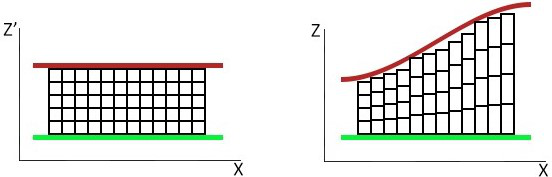
When coordinates are transformed into depositional space their volumetric support also changes. Considering a regular grid in original units, these cells have different volumetric support after transformation, as shown in the figure below (Bertoncello, Caers, Biver, & Caumon, 2008). This issue is usually disregarded and support is assumed to be consistent in both spaces, but this can lead to bias in the final back-transformed results if the change in cell volume varies significantly across the domain. This distortion could lead to possible problems with the reproduction of target statistics, such as the histogram or variogram reproduction.

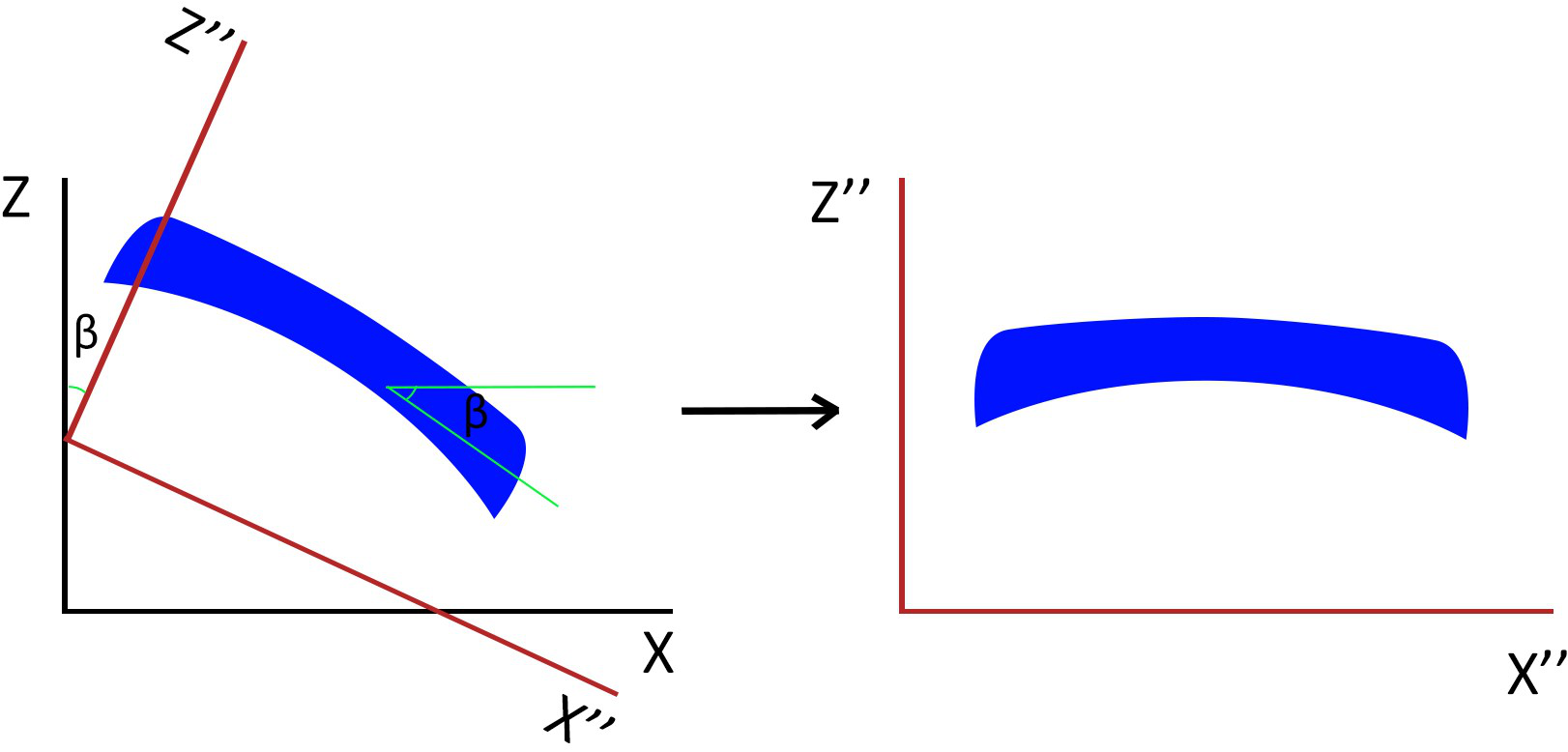
Steeply dipping strata

So far, it has been assumed that the base of the formation is horizontal. However, this is not a requirement for stratigraphic coordinate transformation, the new coordinates could be defined in relation to any arbitrary plane. In the case of large, steeply dipping features, the base of the formation need not be horizontal; the reference plane is tilted or the sample data are rotated to allow for the application of stratigraphic transformations. The following figure demonstrates a dipping stratigraphic formation. Rotating the coordinates by \(\beta\) degrees permits flattening of the original formation, stratigraphic coordinate transformation is now possible (Deutsch, 2015). Rotation can be accomplished by:

\[\begin{bmatrix} x"\\ y"\\ z" \end{bmatrix} = \begin{bmatrix} cos\alpha cos\beta & -cos\beta sin\alpha & -sin \beta \\ sin \alpha & cos \alpha & 0 \\ sin\beta cos\alpha & -sin\beta sin\alpha & cos \beta \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix}\]

In this equation, \(\alpha\) is the strike angle and \(\beta\) is the dip angle of the formation. Rotating the equation system to remove these angles makes transformation easier.

Summary

Stratigraphic coordinate transformation is the process of altering the coordinates of points in space to restore the original spatial continuity of a deformed but generally flat formation. This simple change in coordinates leads to a better quantification of spatial continuity and improves model accuracy. The focus of this lesson was the correlation grids method, which adjusts the elevation of points relative to one bounding surface (truncation/onlap) or two bounding surfaces (proportional). Redefining coordinates requires modeling the correlational surfaces exhaustively in the domain. Realizations of the surfaces should be generated when there is uncertainty in these surfaces. After transforming the coordinates, traditional geostatistical modeling workflows can be implemented in the new coordinates and then back-transformed to the original coordinates after modeling.

References