Learning Objectives

• Review the workflow of conditioning by kriging
• Prove that conditioning by kriging satisfies the requirements of conditional simulation and provides valid conditional realizations

Introduction

Kriging estimation provides the best linear estimate as close as possible to the true unknown value. In kriging, the minimization of the estimation variance involves smoothing the true variability. Kriged estimates honor local data yet the smoothness makes the result inappropriate for transferring uncertainty to calculated response values (e.g., flow simulation). In addition, kriging gives one unique answer, so it is not able to quantify uncertainty. We use simulation to reproduce the variogram and histogram and provide a model of global uncertainty that considers the correct spatial correlation between the simulated values. Simulation samples alternative realizations from a conditional multivariate distribution.

In unconditional simulation, each realization is a sample from the multivariate distribution with the correct variance and the correct covariance between all spatial locations. The unconditional simulation will reproduce the histogram and the spatial variability (variogram) over many realizations. There are an infinite number of possible unconditional realizations, among which the simulations that honor the experimental data values are chosen (Journel & Huijbregts, 1978).

There are two approaches to conditionally simulate from a multivariate distribution. One approach is direct conditional simulation such as sequential simulation, the second is the traditional approach of conditioning unconditional simulated realizations. In this lesson, the procedure of enforcing data reproduction and enforcing correct local conditional distributions, referred to as conditioning, is explained. Conditioning by kriging is of theoretical and practical interest and is used in many places instead of direct methods. Conditioning by kriging primarily provides easier routes to increase computational speed, the ability to use alternative techniques to generate the unconditional realizations, and the ability to independently check and verify histogram/variogram reproduction prior to conditioning. In this lesson, it is proved that this procedure satisfies the requirements of a conditional simulation and thus is a correct approach to condition unconditional realizations.

Assumptions

Consider \(n\) conditioning data sampled as random variables \(Z(\mathbf{u}_\alpha),\alpha=1,...,n\). The set of all random variables at \(n\) sampled and \(N\) unsampled locations, referred to as a random function (RF), \(Z(\mathbf{u}) , \forall \mathbf{u} \in A\), are assumed to belong to the same stationary domain \(A\).

The \((n+N)\)-variate multivariate probability distribution of the RF fully defines the heterogeneity and uncertainty. The simplifying assumption is to use the tractable multivariate Gaussian (MG) distribution as a distribution that is simply and fully parametrized by a vector of \(n+N\) mean values and a \((n+N)\times (n+N)\) covariance matrix. Therefore, the sampled data are transformed to a standard normal Gaussian distribution and everything is back transformed at the end( see the lesson on normal score transform.

The mean value over the domain, \(m\), is stationary and constant at zero. The variance, \(\sigma^2\), is stationary and constant at one everywhere.The covariance matrix is informed by a stationary covariance model, \(C(\mathbf{h})\), or variogram model, \(\gamma(\mathbf{h})\), of the normal scores variables for all possible lag vectors, \(\left \{\mathbf{h=u-u'}, \mathbf{u},\mathbf{u'}\in A\right \}\).

Conditional Simulation and Simple Kriging

Simple kriging (SK) under a MG assumption is equivalent to the normal equations derived by Bayes’ theorem that calculates the conditional distribution moments in sequential Gaussian simulation (Leuangthong, Khan, & Deutsch, 2011). The SK estimate, \(Z_{SK}(\mathbf{u})\), and the SK estimation variance, \(\sigma^2_{SK}(\mathbf{u})\), are the parameters of the conditional Gaussian distribution at location \(\mathbf{u}\), that is, they are equivalent to the conditional mean, \(m_c(\mathbf{u})\), and the conditional variance, \(\sigma^2_c(\mathbf{u})\), given the available data.

\[m_c(\mathbf{u}) = Z_{SK}(\mathbf{u}) = \sum_{\alpha=1}^{n} \lambda_\alpha(\mathbf{u}) Z(\mathbf{u}_\alpha) \hspace{1.0em} (1)\]

\[\sigma^2_c(\mathbf{u}) = \sigma^2_{SK}(\mathbf{u}) = 1-\sum_{\alpha=1}^{n} \lambda_\alpha(\mathbf{u}) C(\mathbf{u}-\mathbf{u}_\alpha) \hspace{1.0em} (2)\]

SK provides the theoretically correct conditional mean and variance. For each unsampled location, \(\mathbf{u}\), the SK equations provide the weights \(\lambda_\alpha(\mathbf{u}), \alpha=1,...,n\):

\[\sum_{\beta=1}^{n} \lambda_\beta(\mathbf{u}) C(\mathbf{u}_\alpha-\mathbf{u}_\beta)= C(\mathbf{u}-\mathbf{u}_\alpha), \alpha=1,...,n \hspace{1.0em} (3)\]

Conditioning By Kriging (CBK)

The first step in carrying out the conditional simulation is to provide an unconditional simulation, \(Z_{us}(\mathbf{u}) , \forall \mathbf{u} \in A\), having the stationary mean and covariance function between all locations. Many methods are available for simulating unconditional realizations, such as turning bands that provides multidimensional simulations for reduced computer costs of one-dimensional simulations (Chiles & Delfiner, 2009). The provided unconditional simulation is conditioned to the experimental data values using the conditioning by kriging (CBK) method.

As shown in Eq.2, the kriging error variance is independent of conditioning data and only depends on the spatial configuration of the conditioning data, hence, the kriging procedure, when applied to the identical data configuration, will result in a same kriging error.

Therefore, given \(Z_{SK}(\mathbf{u})\), kriged from the conditioning data, \(\{Z(\mathbf{u}_\alpha),\alpha=1,...,n\}\), and \(Z_{sk,us}(\mathbf{u})\), kriged from the unconditionally simulated values retained at the locations of the conditioning data, \(\{Z_{us}(\mathbf{u}_\alpha),\alpha=1,...,n\}\), the simulated deviation from kriging is written:

\[[Z_{us}(\mathbf{u})-Z_{sk,us}(\mathbf{u})]\]

The desired conditional simulation, \(Z_{cs}(\mathbf{u})\), is written as

\[Z_{cs}(\mathbf{u}) = Z_{SK}(\mathbf{u}) + [Z_{us}(\mathbf{u})-Z_{sk,us}(\mathbf{u})] \hspace{1.0em}\]

The terms could be reordered for an alternative view of CBK:

\[Z_{cs}(\mathbf{u}) = Z_{us}(\mathbf{u}) + [Z_{SK}(\mathbf{u})-Z_{sk,us}(\mathbf{u})]\]

\[\ = Z_{us}(\mathbf{u}) +\left [ \sum_{\alpha=1}^{n} \lambda_\alpha(\mathbf{u}) Z(\mathbf{u}_\alpha)-\sum_{\alpha=1}^{n} \lambda_\alpha(\mathbf{u}) Z_{us}(\mathbf{u}_\alpha) \right ]\]

\[\ = Z_{us}(\mathbf{u}) +\sum_{\alpha=1}^{n} \lambda_\alpha(\mathbf{u}) [Z(\mathbf{u}_\alpha)-Z_{us}(\mathbf{u}_\alpha)] \]

This view shows that, \(Z_{cs}(\mathbf{u})\) can be obtained by (1) performing an unconditional simulation to obtain \(Z_{us}(\mathbf{u})\), (2) calculate residuals that are the difference between unconditional simulated values retained at the data locations and the original data values themselves, (3) interpolate this residual with simple kriging to get \(Z_{sk}(\mathbf{u})-Z_{sk,us}(\mathbf{u})\), and (4) add the resulting kriged field to the unconditionally simulated field to obtain the conditional simulated values at all locations.

Note that for either view, the kriging setup for CBK is simple kriging with a large search, all of the samples that influence the kriged estimates (25 to 50) and a variogram consistent with the data and the unconditional simulation. The kriging estimates, \(Z_{sk,us}(\mathbf{u})\) and \(Z_{SK}(\mathbf{u})\), as well as \(Z_{us}(\mathbf{u})\) must use the same normal scores variogram. The corresponding covariance function \(C(\mathbf{h})= 1-\gamma(\mathbf{h})\) is used in kriging, simulation and theoretical development. Because of the exactitude property of kriging, \(Z_{cs}(\mathbf{u})\) honors the data at the data locations.

Theory of CBK

CBK requires valid unconditional simulation that correctly satisfies the stationary limit properties. The unconditional simulation has the stationary mean of zero and the stationary covariance function, \(C(\mathbf{h})\), between all locations (Chiles & Delfiner, 2009; Journel, 1989).

(Johnson & Wichern, 2008) prove that conditional Gaussian distributions are defined by the following properties,

1. \(Mean=m_c(\mathbf{u}) ,\hspace{1.0em}\forall \mathbf{u} \in A\)
2. \(Variance=\sigma^2_c(\mathbf{u}) ,\hspace{1.0em} \forall \mathbf{u} \in A\)
3. \(Covariance=C(\mathbf{u}-\mathbf{{u}'})-\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha(\mathbf{u}) \lambda_\beta(\mathbf{{u}'}) C(\mathbf{u}_\alpha - \mathbf{u}_\beta) ,\hspace{1.0em} \forall \mathbf{u},\mathbf{{u}'} \in A\)

where the conditional mean, \(m_c(\mathbf{u})\), and the conditional variance, \(\sigma^2_c(\mathbf{u})\) were introduced in Eq.1 and Eq.2.

These are three requirements that conditional realizations must satisfy. Beyond this, the shapes of all distributions must be Gaussian, but this is enforced by the central limit theorem. The proof that CBK satisfies these requirements is provided below. The relation in Eq.6 as derived below is useful for the proof:

The kriged estimate is too smooth because its variance is too small. This is proved that the missing variance is the SK estimation variance. The variance of kriged estimate equals to the stationary variance minus the SK estimation variance:

\[var\{m_c(\mathbf{u})\}=E\{m_c^2(\mathbf{u})\}-[E\{m_c(\mathbf{u})\}]^2\]

\[=E\left\{\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha \lambda_\beta Z(\mathbf{u}_\alpha) Z(\mathbf{u}_\beta \right\} - \left [ E\left \{ \sum_{\alpha=1}^{n} \lambda_\alpha Z(\mathbf{u}_\alpha) \right \} \right ]^2\]

\[\ =\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha \lambda_\beta E\left \{ Z(\mathbf{u}_\alpha) Z(\mathbf{u}_\beta) \right \} -\left [ \sum_{\alpha=1}^{n} \lambda_\alpha E\left \{ Z(\mathbf{u}_\alpha) \right \} \right ]^2\]

\[var\{m_c(\mathbf{u})\}=\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha \lambda_\beta C(\mathbf{u}_\alpha-\mathbf{u}_\beta) \hspace{1.0em} (4)\]

Substituting, Eq.3, into Eq.2 results in,

\[\sigma^2_c(\mathbf{u})=1-\sum_{\alpha=1}^{n}\sum_{\beta=1}^{n} \lambda_\alpha \lambda_\beta C(\mathbf{u}_\alpha-\mathbf{u}_\beta) \hspace{1.0em} (5)\]

Substituting Eq.5 into Eq.4 results in,

\[var\{m_c(\mathbf{u})\}=1-\sigma^2_c(\mathbf{u}) \hspace{1.0em} (6)\]

1. Conditional Mean

Mean of \(Z_{cs}(\mathbf{u})\) at each simulated location equals to the conditional mean at that location:

\[E\left \{ Z_{cs}(\mathbf{u})\right \}= E\left \{ Z_{sk}(\mathbf{u})+ \left [ Z_{us}(\mathbf{u})-Z_{sk,us}(\mathbf{u}) \right ]\right \} \]

\[ = Z_{sk}(\mathbf{u})+E\left \{ Z_{us}(\mathbf{u})\right \}-E\left \{ Z_{sk,us}(\mathbf{u})\right \}\]

Substituting, \(E\left \{ Z_{us}(\mathbf{u})\right \}=0\),

\[=Z_{sk}(\mathbf{u})-E\left \{ \sum_{\alpha=1}^{n} \lambda_\alpha Z_{us}(\mathbf{u}_\alpha)\right \} \]

\[=Z_{sk}(\mathbf{u})- \sum_{\alpha=1}^{n} \lambda_\alpha E\left \{ Z_{us}(\mathbf{u}_\alpha) \right \} \]

\[E\left \{ Z_{cs}(\mathbf{u})\right \}=Z_{sk}(\mathbf{u})=m_c(\mathbf{u}) \hspace{1.0em} \forall \mathbf{u} \in A\]

2. Conditional Variance

The variance of \(Z_{cs}(\mathbf{u})\) at each simulated location equals the conditional variance at that location:

\[var\left \{ Z_{cs}(\mathbf{u}) \right \} =E\left \{ \left [ Z_{cs}(\mathbf{u})-E\left \{ Z_{cs}(\mathbf{u})\right \} \right ]^2 \right \} \]

\[=E\left \{ \left [Z_{cs}(\mathbf{u})-Z_{sk}(\mathbf{u}) \right ]^2 \right \} \]

\[=E\left \{ \left [Z_{sk}(\mathbf{u})+Z_{us}(\mathbf{u})-Z_{sk,us}(\mathbf{u})-Z_{sk}(\mathbf{u})\right ]^2 \right \} \]

\[=E\left \{ \left [Z_{us}(\mathbf{u})-Z_{sk,us}(\mathbf{u})\right ]^2 \right \} \]

\[=E\left \{ \left [ Z_{us}(\mathbf{u}) \right ]^2 \right \}-2E\left \{ Z_{us}(\mathbf{u}) Z_{sk,us}(\mathbf{u}) \right \} +E\left \{ \left [ Z_{sk,us}(\mathbf{u}) \right ]^2 \right \} \hspace{1em}\]

Substituting, \(E\left \{ \left [ Z_{sk,us}(\mathbf{u}) \right ]^2 \right \}=1-\sigma^2_c(\mathbf{u})\) (as proved in Eq.6) and substituting \(E\left \{ \left [ Z_{us}(\mathbf{u}) \right ]^2 \right \}=1\),

\[var\left \{ Z_{cs}(\mathbf{u}) \right \} = 1-2\sum_{\alpha=1}^{n} \lambda_\alpha E\left \{ Z_{us}(\mathbf{u}) Z_{us}(\mathbf{u}_\alpha) \right \} +1-\sigma^2_c(\mathbf{u})\]

\[=1-2\sum_{\alpha=1}^{n} \lambda_\alpha C(\mathbf{u},\mathbf{u}_\alpha) +1-\sigma^2_c(\mathbf{u})\]

\[=1-2(1-\sigma^2_c(\mathbf{u}))+1-\sigma^2_c(\mathbf{u})\]

\[var\left \{ Z_{cs}(\mathbf{u}) \right \}=\sigma^2_c(\mathbf{u})=\sigma^2_{SK}(\mathbf{u})\]

3. Conditional Covariance

The covariance between two conditionally simulated points equals to the stationary covariance model, \(C(h)\), minus the covariance between the conditioning data.

\[ Z_{cs}(\mathbf{u}) = Z_{sk}(\mathbf{u}) + \left [ Z_{us}(\mathbf{u})-Z_{sk,us}(\mathbf{u}) \right ] \]

\[ Z_{cs}(\mathbf{{u}'}) = Z_{sk}(\mathbf{{u}'}) + \left [ Z_{us}(\mathbf{{u}'})-Z_{sk,us}(\mathbf{{u}'}) \right ] \]

\[cov\left \{Z_{cs}(\mathbf{u}) ,Z_{cs}(\mathbf{{u}'})\right \} =E\left \{ \left [ Z_{cs}(\mathbf{u})-E\left \{ Z_{cs}(\mathbf{u}) \right \} \right ] \left [ Z_{cs}(\mathbf{{u}'})-E\left \{ Z_{cs}(\mathbf{{u}'}) \right \} \right ] \right \} \]

\[ =E \left \{ \left [ Z_{cs}(\mathbf{u})-Z_{sk}(\mathbf{u}) \right ] \left [ Z_{cs}(\mathbf{{u}'})-Z_{sk}(\mathbf{{u}'}) \right ] \right \} \]

\[= E \left \{ \left [ Z_{us}(\mathbf{u})-Z_{sk,us}(\mathbf{u}) \right ] \left [ Z_{us}(\mathbf{{u}'})-Z_{sk,us}(\mathbf{{u}'}) \right ] \right \} \]

\[=\left \{ \color{magenta}{Z_{us}(\mathbf{u}) Z_{us}(\mathbf{{u}'})}-\color{green}{Z_{sk,us}(\mathbf{u}) Z_{us}(\mathbf{{u}'})}-\color{blue}{Z_{us}(\mathbf{u}) Z_{sk,us}(\mathbf{{u}'})}+ \color{red}{Z_{sk,us}(\mathbf{u}) Z_{sk,us}(\mathbf{{u}'})} \right \} \hspace{1.0em} (7)\]

Given that \(Z_{sk,us}(\mathbf{u})=\sum_{\alpha=1}^{n}\lambda_\alpha(\mathbf{u}) Z_{us}(\mathbf{u}_\alpha)\) and \(Z_{sk,us}(\mathbf{{u}'})=\sum_{\alpha=1}^{n}\lambda_\alpha(\mathbf{{u}'}) Z_{us}(\mathbf{u}_\alpha)\), Eq.7 becomes,

\[cov\left \{Z_{cs}(\mathbf{u}) ,Z_{cs}(\mathbf{{u}'})\right \} = \color{magenta}{C(\mathbf{u}-\mathbf{{u}'})} -\color{green}{\sum_{\alpha=1}^{n} \lambda_\alpha(\mathbf{u}) E\left \{ Z_{us}(\mathbf{u}_\alpha) Z_{us}(\mathbf{{u}'}) \right \}} \]

\[-\color{blue}{\sum_{\alpha=1}^{n} \lambda_\alpha(\mathbf{{u}'}) E\left \{ Z_{us}(\mathbf{u}) Z_{us}(\mathbf{u}_\alpha) \right \}} +\color{red}{\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha(\mathbf{u}) \lambda_\beta(\mathbf{{u}'}) E\left \{ Z_{us}(\mathbf{u}_\alpha) Z_{us}(\mathbf{u}_\beta) \right \}}\]

\[cov\left \{Z_{cs}(\mathbf{u}) ,Z_{cs}(\mathbf{{u}'})\right \} = \color{magenta}{C(\mathbf{u}-\mathbf{{u}'})} -\color{green}{\sum_{\alpha=1}^{n} \lambda_\alpha(\mathbf{u}) C(\mathbf{u}_\alpha-\mathbf{{u}'})} -\color{blue}{\sum_{\alpha=1}^{n} \lambda_\alpha(\mathbf{{u}'}) C(\mathbf{u}-\mathbf{u}_\alpha)}\]

\[+\color{red}{\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha(\mathbf{u}) \lambda_\beta(\mathbf{{u}'}) C(\mathbf{u}_\alpha - \mathbf{u}_\beta)}\]

Given that,

\[ \sum_{\beta=1}^{n} \lambda_\beta(\mathbf{u}) C(\mathbf{u}_\alpha - \mathbf{u}_\beta) =C(\mathbf{u} - \mathbf{u}_\alpha), \hspace{1.0em} \forall \mathbf{u}_\alpha \]

\[ \sum_{\beta=1}^{n} \lambda_\beta(\mathbf{{u}'}) C(\mathbf{u}_\alpha - \mathbf{u}_\beta) =C(\mathbf{{u}'} - \mathbf{u}_\alpha), \hspace{1.0em} \forall \mathbf{u}_\alpha \]

\[cov\left \{Z_{cs}(\mathbf{u}) ,Z_{cs}(\mathbf{{u}'})\right \} =\color{magenta}{C(\mathbf{u}-\mathbf{{u}'})} -\color{green}{\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha(\mathbf{u}) \lambda_\beta(\mathbf{{u}'}) C(\mathbf{u}_\alpha - \mathbf{u}_\beta)}\]

\[-\color{blue}{\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha(\mathbf{{u}'}) \lambda_\beta(\mathbf{u}) C(\mathbf{u}_\alpha - \mathbf{u}_\beta)} -\color{red}{\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha(\mathbf{u}) \lambda_\beta(\mathbf{{u}'}) C(\mathbf{u}_\alpha - \mathbf{u}_\beta)}\]

\[cov\left \{Z_{cs}(\mathbf{u}) ,Z_{cs}(\mathbf{{u}'})\right \} =C(\mathbf{u}-\mathbf{{u}'}) -\sum_{\alpha=1}^{n} \sum_{\beta=1}^{n} \lambda_\alpha(\mathbf{u}) \lambda_\beta(\mathbf{{u}'}) C(\mathbf{u}_\alpha - \mathbf{u}_\beta) \hspace{1.0em} \forall \mathbf{u},\mathbf{{u}'} \in A\]

This proves that in presence of the conditioning data, the covariance between two conditionally simulated points is (1) correct-see above, and (2) less than the stationary covariance. It is also intuitively accepted because conditioning to data constrains the uncertainty. Thereby, conditional simulation does not exactly reproduce the input variogram model.

Examples

To illustrate the CBK steps of making conditional simulations using simple kriging, a one-dimensional and a two-dimensional example of several realizations are explored below. In the given dataset the spatial random variable is top elevation of a reservoir surface.

The following figure shows CBK conditional simulation obtained by an unconditional sequential Gaussian simulation (SGSIM), SK of conditioning data points and SK of unconditionally simulated values at these data locations.

Readers using a web-browser may use the slider at the bottom to view different realizations.

In the 1D example shown in the above figure, the plots illustrate steps outlined in the first view of CBK. In this dataset, there are five well data points stochastically distributed in the first half of the domain length of \(1000m\) and no conditioning data in the right side. With the last data point at \(500m\), it has influense up to \(500m\) plus range of about \(200m\) and thus on the far of right side, the SK model at distances greater than the range is equal to the global mean of zero and the residual is zero. Therefore, the conditional relization becomes exactly the same as the unconditional realization which does not meet the heterogeneity of the inaccessible truth phenomenon from which the five conditioning data were sampled.

In the first half of the domain, compared to the kriging estimation curve, the conditioned simulation curve by CBK is a better reproduction of fluctuations of the unknown truth.

The Kriged estimates from the conditioning data and from unconditionally simulated values at data locations exactly honor the data values and unconditional values respectively.

The next Figure illustrates a 2D example. The maps of kriged estimates minimize the square variance and thus are rather smooth compared to the simulation maps. Although the variogram modeled from the conditioning (reference) data is used to make a kriging estimate, the variogram of the kriged estimates would not reproduce the reference variogram.

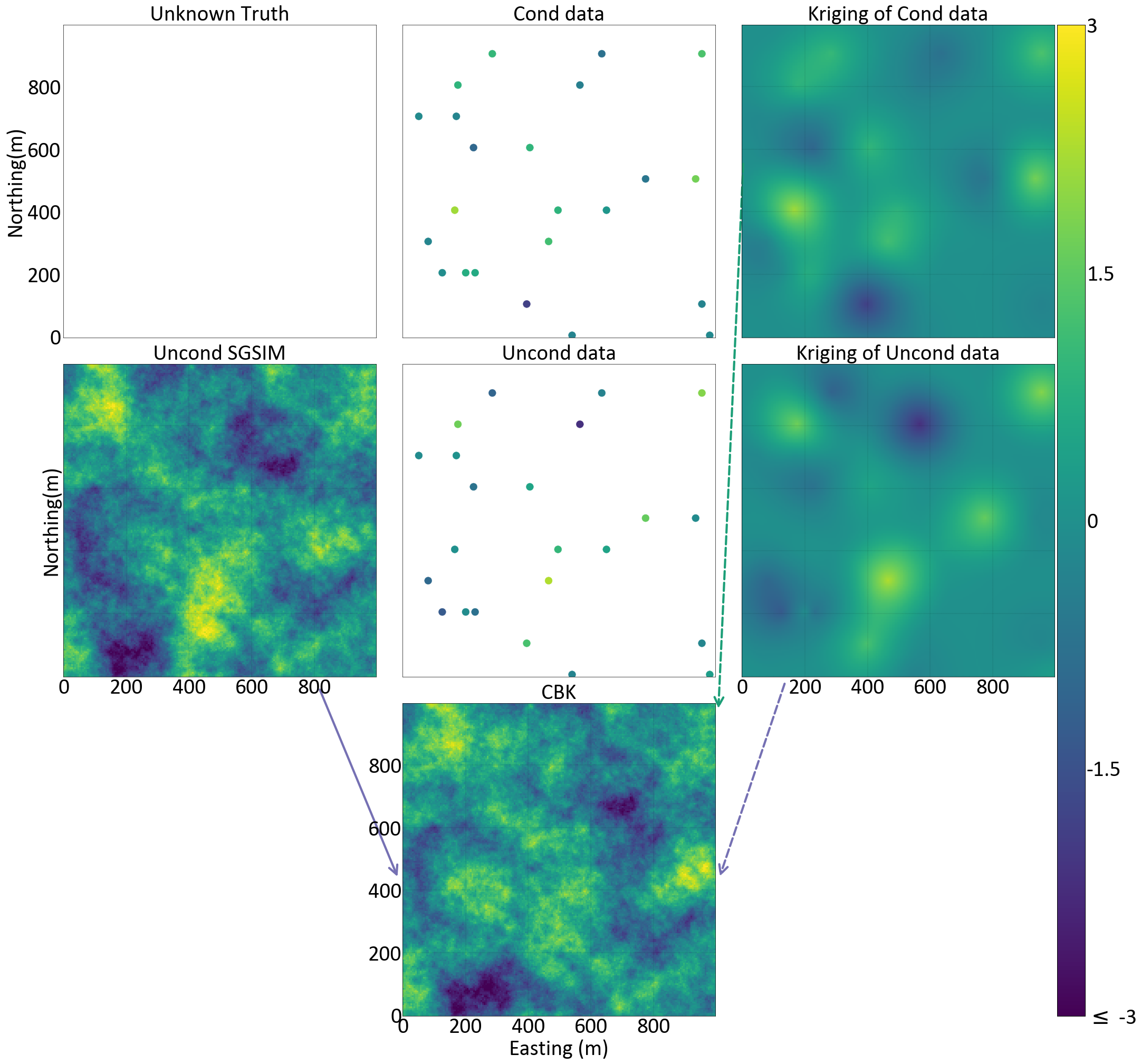
Conclusion

The marginal distributions of our MG distribution are standard normal Gaussian; however, the conditional distributions of MG at the unsampled locations conditioned to data are not standard Gaussian because of the conditioning by data, but they are still Gaussian. As a result, the unconditional simulation will reproduce the stationary mean of zero, the stationary variance of one and the stationary covariance model, thus exactly reproduces the input variogram model produced by the conditioning data. However, when we condition them to the data, due to honoring the conditional data, the conditional variance at data points is zero and it increases away from data. Therefore, unconditionally simulated realizations satisfy stationary limit properties and the conditional simulation obtained by CBK satisfies the correct conditional properties and is theoretically correct.

At each grid node, the CBK procedure is repeated with many alternative unconditional realizations in order to provide many conditional realizations. The kriging weights calculated for each grid node are independent of data values (and unconditionally simulated values) and only depend on the spatial configuration of the data and grid node, hence, the kriging weights do not change for all realizations at each grid node. Thereby, computational efficiencies could be gained by saving the weights or processing multiple realizations simultaneously.

On the other hand, formulating the kriging in a dual formulation is very efficient and is highly recommended for the conditioning, because then the kriging equations are solved once and it is very fast. However, it would have to be solved again for each realization since the unconditionally simulated values are embedded in the dual kriging weights. A dual formalism to the SK system is an alternative formulation where the dual kriging weights are independent of spatial configuration of grid nodes and only depend on the spatial configuration of data and data values. Instead of being a linear combination of the \(n\) data \((Z(\mathbf{u}_\alpha) – m)\), the dual SK estimate is formulated as a linear combination of \(n\) data-to-unknown covariance functions, \(C(\mathbf{u}-\mathbf{u}_\alpha)\).

References