Learning Objectives

• Understand the place of bootstrap resampling.
• Appreciate the need for the multivariate spatial bootstrap in the context of geostatistical modeling.
• Consolidate understanding of the technique with application to a vein modeling dataset.

Introduction

Accurate characterization of uncertainty in mineral resources is one of the main objectives of geostatistics. Uncertainty in resource estimates provides more complete information to decision making.

Conditional simulation techniques are used to generate realizations that represent variability and uncertainty. Large-scale uncertainty in the resources can be underestimated if uncertainty in the global input histogram is not considered (Khan & Deutsch, 2016).

The uncertainty in the global histogram parameters is established by using the bootstrap to resample the input histogram, followed by simulation of realizations (Deutsch, 2004). Uncertainty in domain boundary locations, the variogram, and other parameters could be considered, but this Lesson focuses on the global histogram.

Review of the Bootstrap Methodology

To assess the uncertainty in the global histogram, a variant of the bootstrap technique pioneered by (Efron, 1982) is employed. The bootstrap utilizes Monte Carlo simulation to resample \(n\) data values to create different distributions of data. The distributions of data can be summarized by their mean and variance. The recommended approach is to use realizations of the distributions in subsequent geostatistical modeling.

The bootstrap methodology for uncertainty in the experimental mean is summarized as follows: (1) perform declustering to create a representative distribution \((F_Z(z))\), (2) draw \(n\) values using replacement (equal to the number of available data) using uniformly distributed random numbers, \(p_i, \; i=1,...n\), and record the corresponding quantiles: \(z_i = F_Z^{-1}(p_i), \; i=1,...n\), (3) calculate the experimental mean of the new distribution, and (4) return to step (2) to generate many realizations of the mean for a stable distribution. Thousands of realizations are typically generated.

The resampled distributions of \(n\) data could be retained for the calculation of other statistics or for input to geostatistical calculations. The bootstrap assumes samples are independent and that the underlying histogram of the data is representative of the population. In geological applications, the data almost always show spatial correlation. The bootstrap was modified to consider the spatial correlation between data by several authors including Solow (1985), Deutsch (2004), and Journel & Bitanov (2004).

Multivariate Spatial Bootstrap Methodology

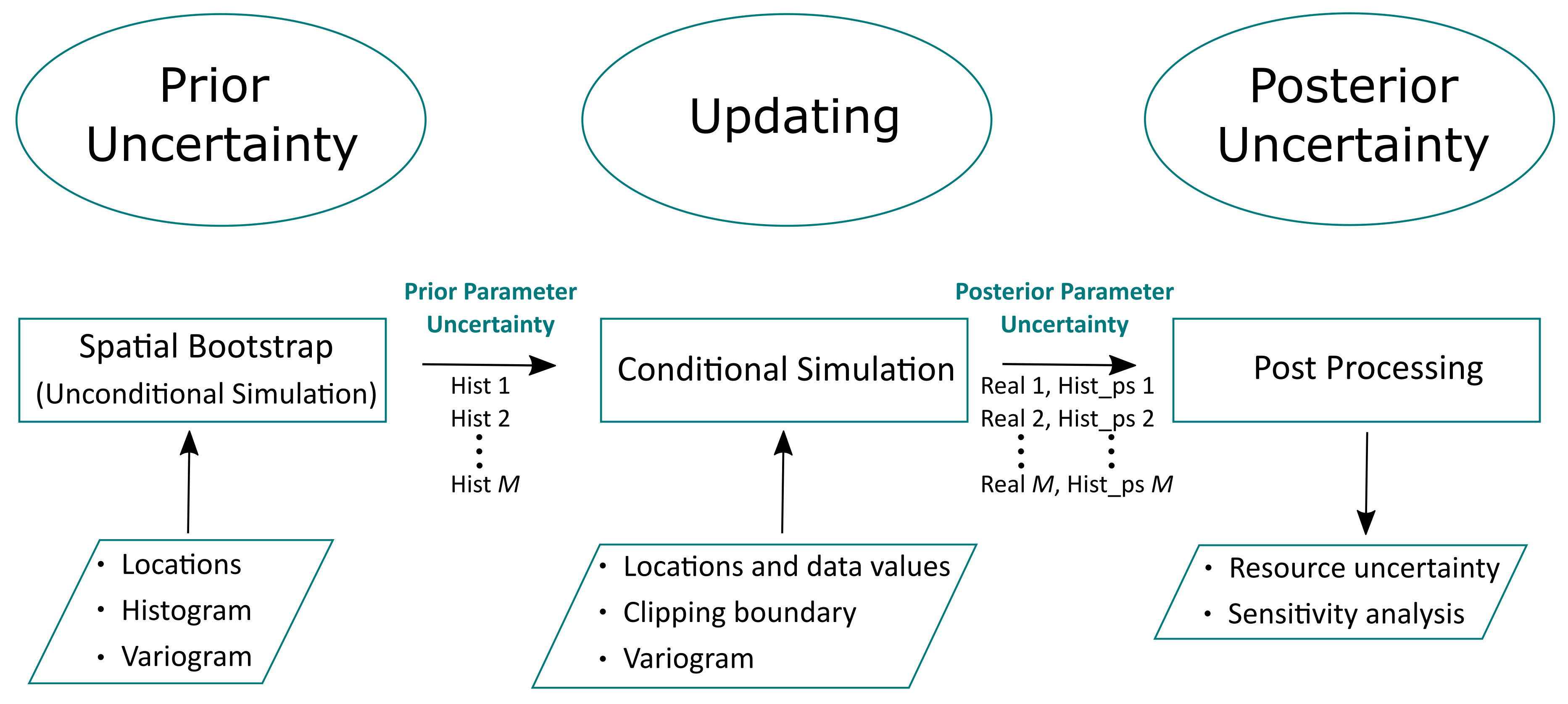
The multivariate spatial bootstrap differs from the standard bootstrap by considering the spatial correlation of \(K\) geological variables sampled at \(n\) data locations \(z_k(\mathbf{u}_i), \; i=1,...,n, \; k = 1,...,K\) with a geostatistical simulation algorithm. The conditioning data and the domain limits are not considered. A set of data with greater spatial correlation have higher uncertainty because the data are more redundant (Khan & Deutsch, 2016). The spatial bootstrap realizations represent the prior parameter uncertainty in the histogram before updating with the conditioning data and the domain limits. The LU simulation method is often chosen because it is simple and efficient for a large number of realizations and for data sets not exceeding about 5,000 locations. An alternative simulation algorithm such as sequential Gaussian simulation would be used for larger data sets.

Conditioning of the spatial bootstrap realizations by the input data during simulation and then clipping by the domain boundary yields the posterior histogram uncertainty. This has been shown to correctly transfer uncertainty in the histogram. The following describes the procedure for the multivariate case of the spatial bootstrap (Rezvandehy, 2016):

\(\textbf{Prior Uncertainty}\)

1. Define a representative histogram of the \(n\) composited input data for each random variable \(F_{Z_k}(z_k)\) (see Lesson on declustering).

2. Transform the representative histogram data \(F_{Z_k}(z_k)\) to Gaussian units \(G_{Y_k}(y_k)\) through the quantile transform \(y_{k,i} = G^{-1}_{Y_k}(F_{Z_k}(z_{k}))\).

3. Model the direct and cross variograms between all variables \(\gamma_{Y_{kk^{\prime}}}(\mathbf{h})\) in Gaussian units. The linear model of coregionalization or a simpler intrinsic model of coregionalization could be considered. The \(k\) and \(k^\prime\) subscripts denote the RV representing the two variables in the cross variogram. For \(K\) random variables, there are a total of \(K(K+1)/2\) direct and cross variograms.

4. Perform a Cholesky LU decomposition of the covariance matrix as \(\mathbf{C} = \mathbf{LL}^T\), where \(\mathbf{C}\), \(\mathbf{L}\) and \(\mathbf{L}^T\) are \(nK\)-by-\(nK\) matrices. \(\mathbf{L}\) is the lower triangular matrix and \(\mathbf{L}^T\) is its transpose.

5. Generate \(M\) unconditional realizations by multiplying the \(\mathbf{L}\) matrix by \(\mathbf{w}\), a \(nK\)-by-\(1\) vector of independent Gaussian deviates (generated in the same manner as Step 2 in the Bootstrap section above): \[\mathbf{y}^{(m)} = \mathbf{Lw}^{(m)}, \; m=1,...,M\] where \(\mathbf{y}\) is the resulting \(nK\)-by-1 vector of unconditionally simulated Gaussian values with the correct correlation over \(M\) realizations.

6. Backtransform each value with the correct global back transformation table. There are \(K\) backtransform tables.

7. Generate the distribution of uncertainty in the parameter of interest for each RV (e.g., mean, variance, correlation, etc.).

\(\textbf{Posterior Uncertainty}\)

8. Using the spatial bootstrap realizations as reference distributions, perform a normal-score transform of the original input data \(M\) times. Keep the \(M\) transform tables for back transformation in Step 9 (see Lesson on the normal score transform).

9. Perform \(M\) conditional simulations of the multivariate data using the transformed data from Step 8 and then backtransform each realization to original units using the transform tables from the previous step.

10. Clip the realizations to the domain limits.

The spatial bootstrap process is sketched:

Example

Input Data

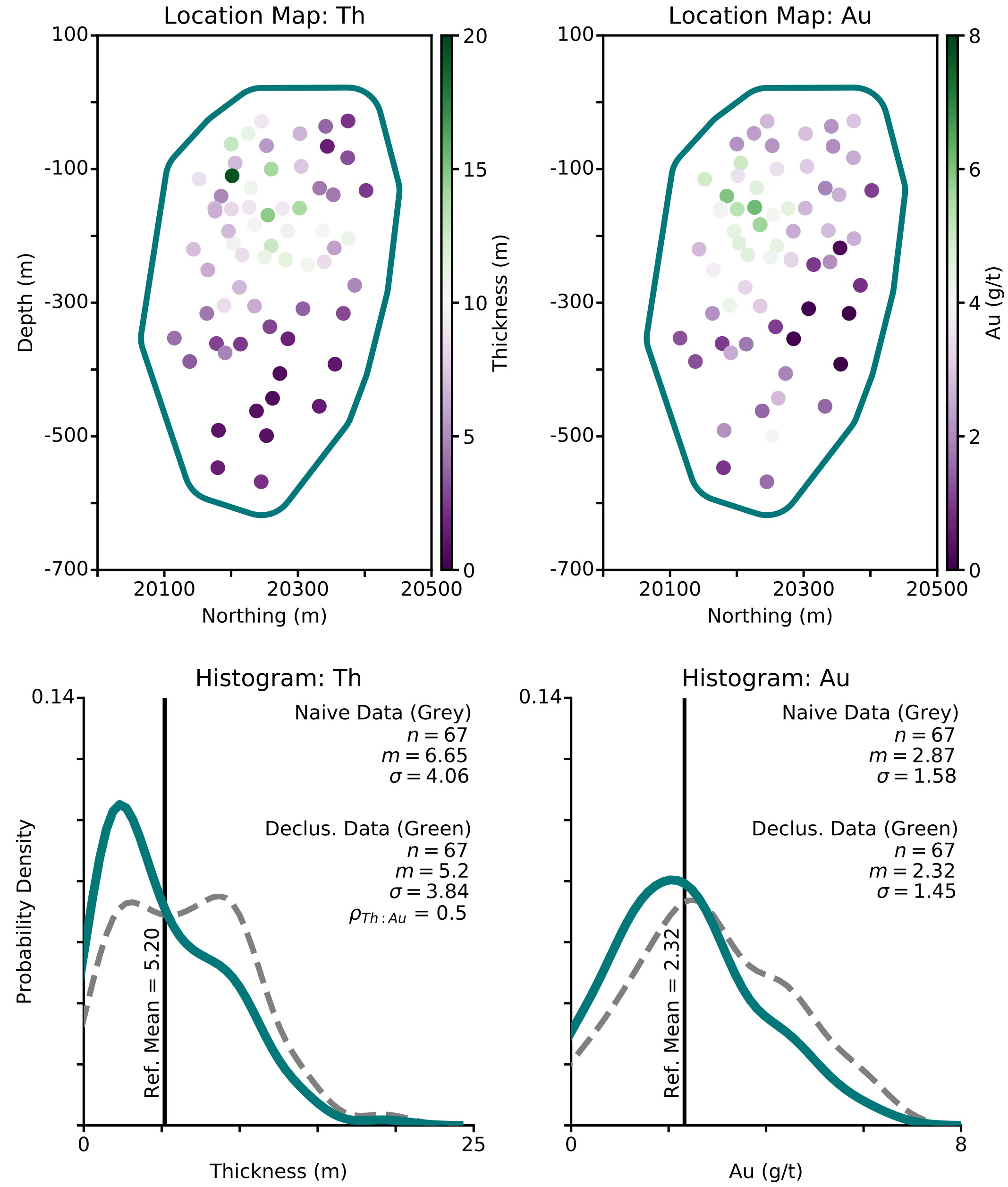
The following example utilizes a two-dimensional, multivariate geological data set containing \(n = 67\) composited drill hole data. Compositing ensures the samples are equally weighted. The data are bounded by a \(50m\) domain clipping limit (Figure 2). The variables of interest are thickness (\(Th\)) and gold (\(Au\)) (\(K = 2\)). They are spatially correlated (\(\rho_{Th:Au} = 0.50\)), with higher values generally located in the upper half of the domain. Declustering was undertaken using a \(90m\) x \(90m\) grid to generate the representative distributions.

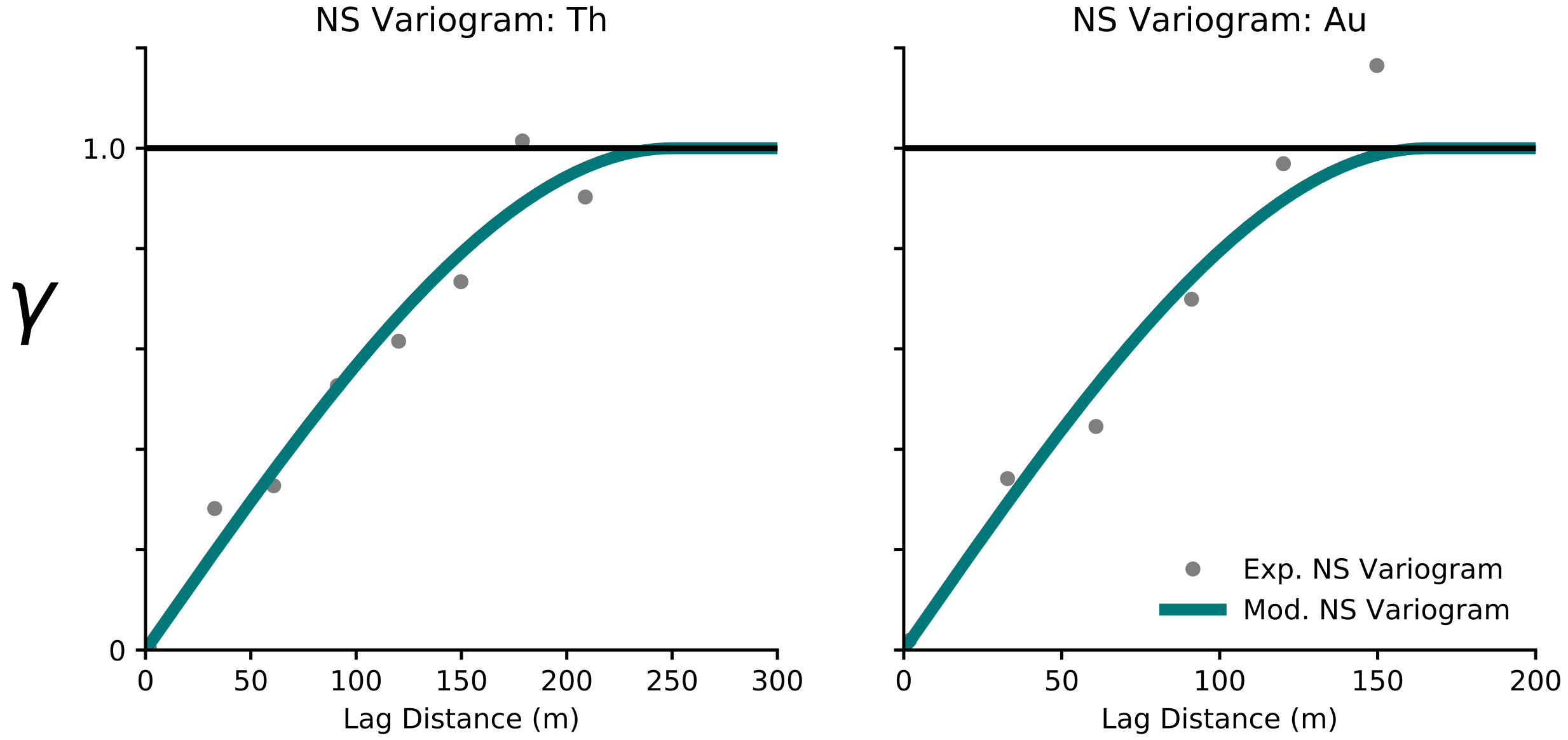
The data are normal-score transformed for variogram modeling and spatial bootstrap resampling. The direct experimental variograms are modeled using a single spherical structure, with ranges of \(250m\) and \(165m\) for \(Th\) and \(Au\) respectively (Figure 3). An intrinsic model of coregionalization is used to scale the cross-covariance between the two variables. A range of \(250m\) is used for both \(Th\) and \(Au\) in this step because \(Th\) is the primary variable of interest.

Prior Histogram Uncertainty

Unconditional LU simulation is used to simulate \(M = 200\) realizations of the declustered \(Th\) and \(Au\) distributions, each containing \(n = 67\) data points. These are displayed as the green lines in the cumulative probability plots in the upper graphs of Figure 4. The variability of these realizations reflects the resampling of the drill holes considering only the data locations and the covariance, not the data values or the domain limits.

Each realization is averaged to create a distribution of 200 mean values that are plotted in the bottom of Figure 4. These histograms represent the prior uncertainty distributions of each variable. The mean values of \(Th\) and \(Au\) compare very closely to the mean values of the declustered distributions. The uncertainty in the histograms is large due to the correlation of \(Th\) and \(Au\). Recall that higher correlation between variables means the data are more redundant and therefore increase uncertainty. A lower \(\rho_{Th:Au}\) would have yielded a narrower prior distribution of uncertainty.

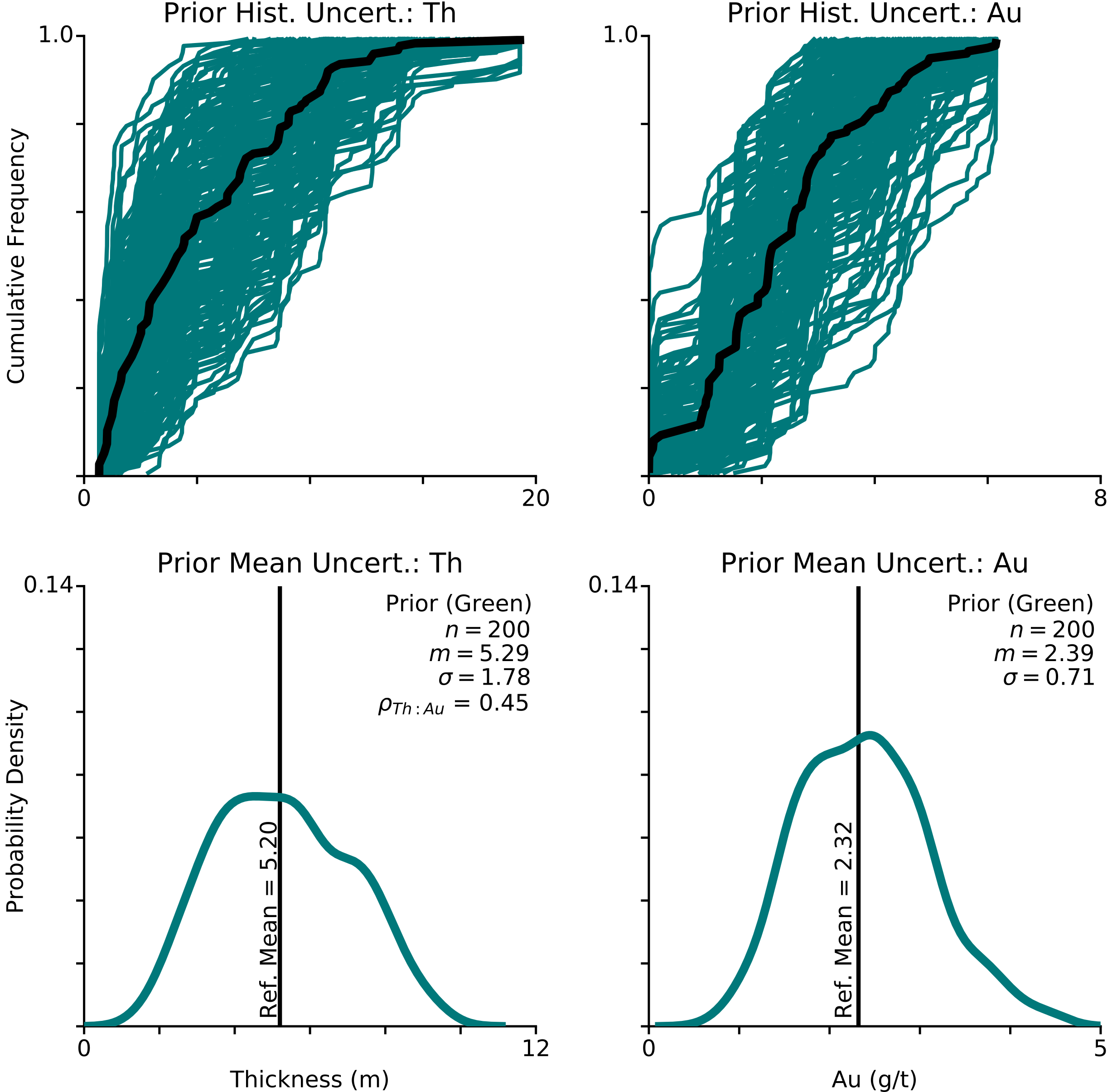
The average correlation of \(Th\) and \(Au\) from each realization is calculated. The distribution of the averages has a mean of \(\rho_{Th:Au} = 0.45\), which demonstrates the spatial relationship is respected during simulation.

Posterior Histogram Uncertainty

Updating of the prior histogram uncertainty to the posterior histogram uncertainty is achieved through application of the conditioning data and the domain clipping limits during simulation. Before simulation, each spatial bootstrap realization is used as a reference distribution during the normal-score transform of the declustered data.

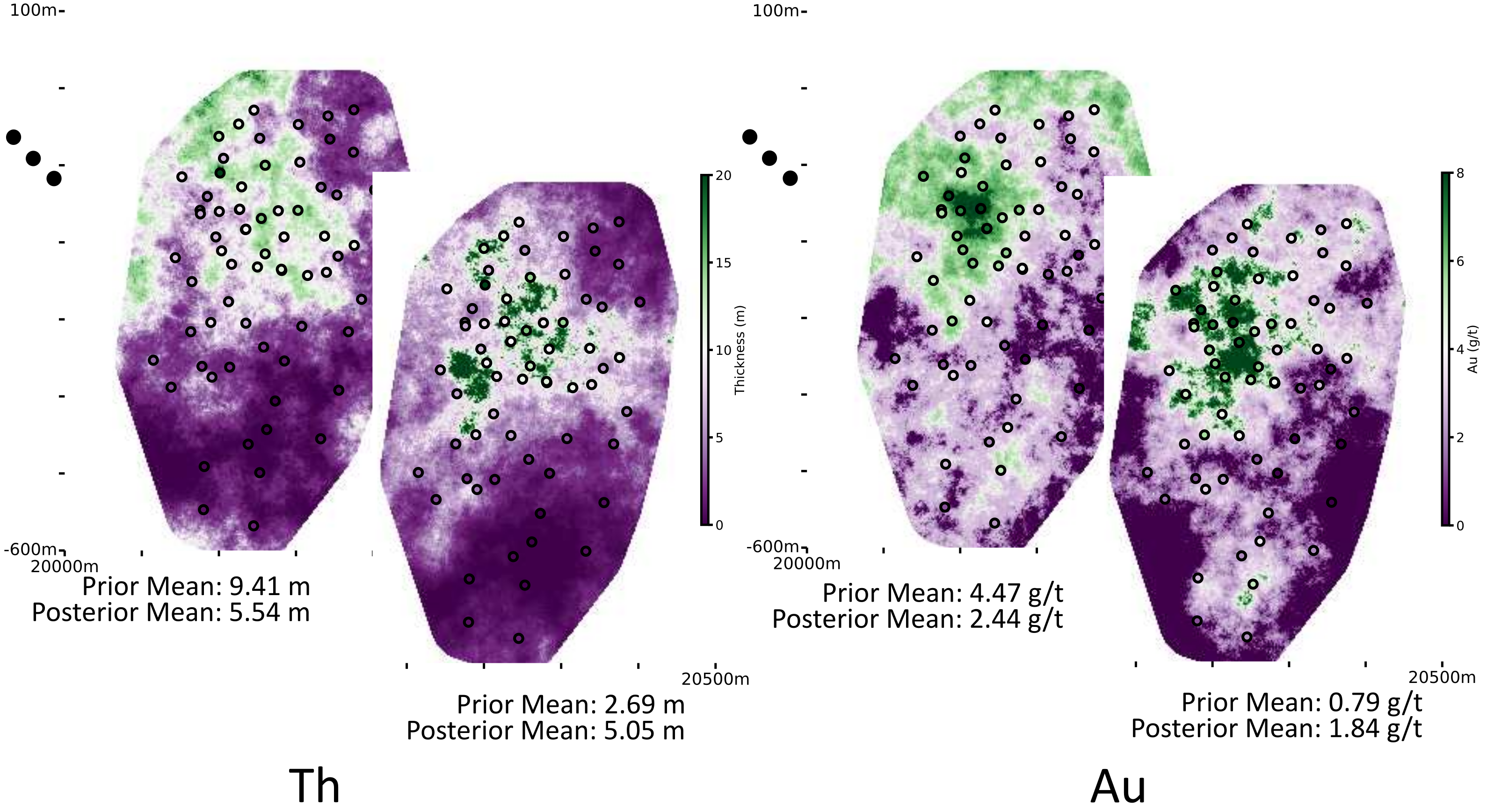
The \(Th\) variable is simulated independently using the modeled variogram parameters from Figure 3, then \(Au\) is simulated using the variogram model from Figure 3 with the \(Th\) realizations acting as secondary data during co-simulation (Figure 5). The \(50m\) clipping limit is applied before backtransforming the realizations using the spatial bootstrap reference distributions. It is through this forward and backward transformation process that the variance from the spatial bootstrap is transferred to update the conditioning data.

The \(Th\) and \(Au\) realizations in Figure 5 represent the highest and lowest average histogram realization from the prior uncertainty distribution (Figure 4). Application of the conditioning data and clipping limits to yield the posterior uncertainty distribution demonstrates the effect on the means of the distributions.

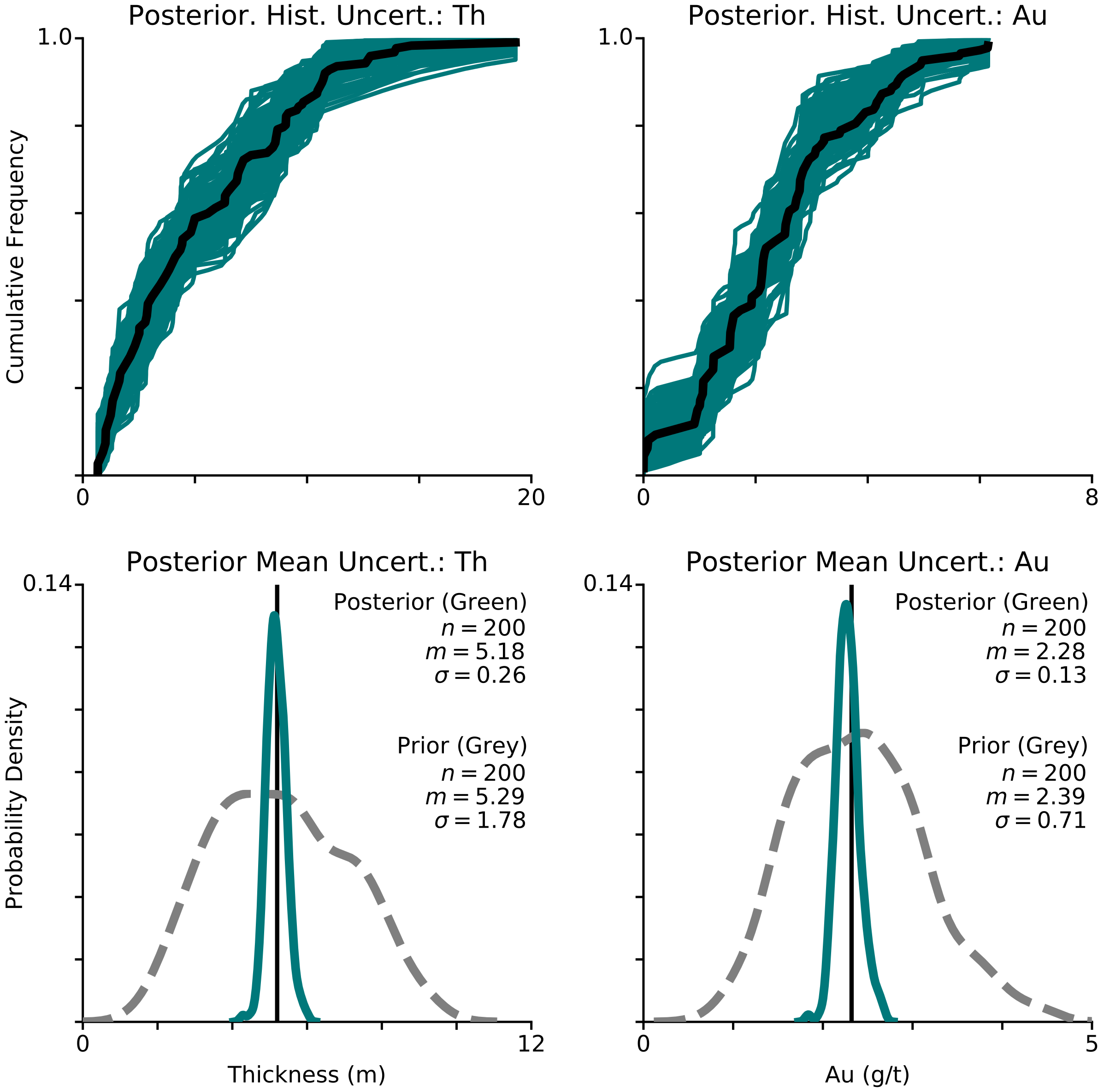
The results of the \(Th\) and \(Au\) realizations are plotted as green lines in the upper graphs of Figure 6. The declustered reference distributions are the black lines. There is a significant reduction in the variance of the realizations in comparison to the spatial bootstrap realizations, which is the result of the conditioning data and clipping limits. The distributions of the means of the realizations are plotted in the lower graphs in green. For comparison, the gray dashed lines represent the prior histogram uncertainty distributions from Figure 4. The vertical black lines are from the declustered input data.

Sensitivity Analysis

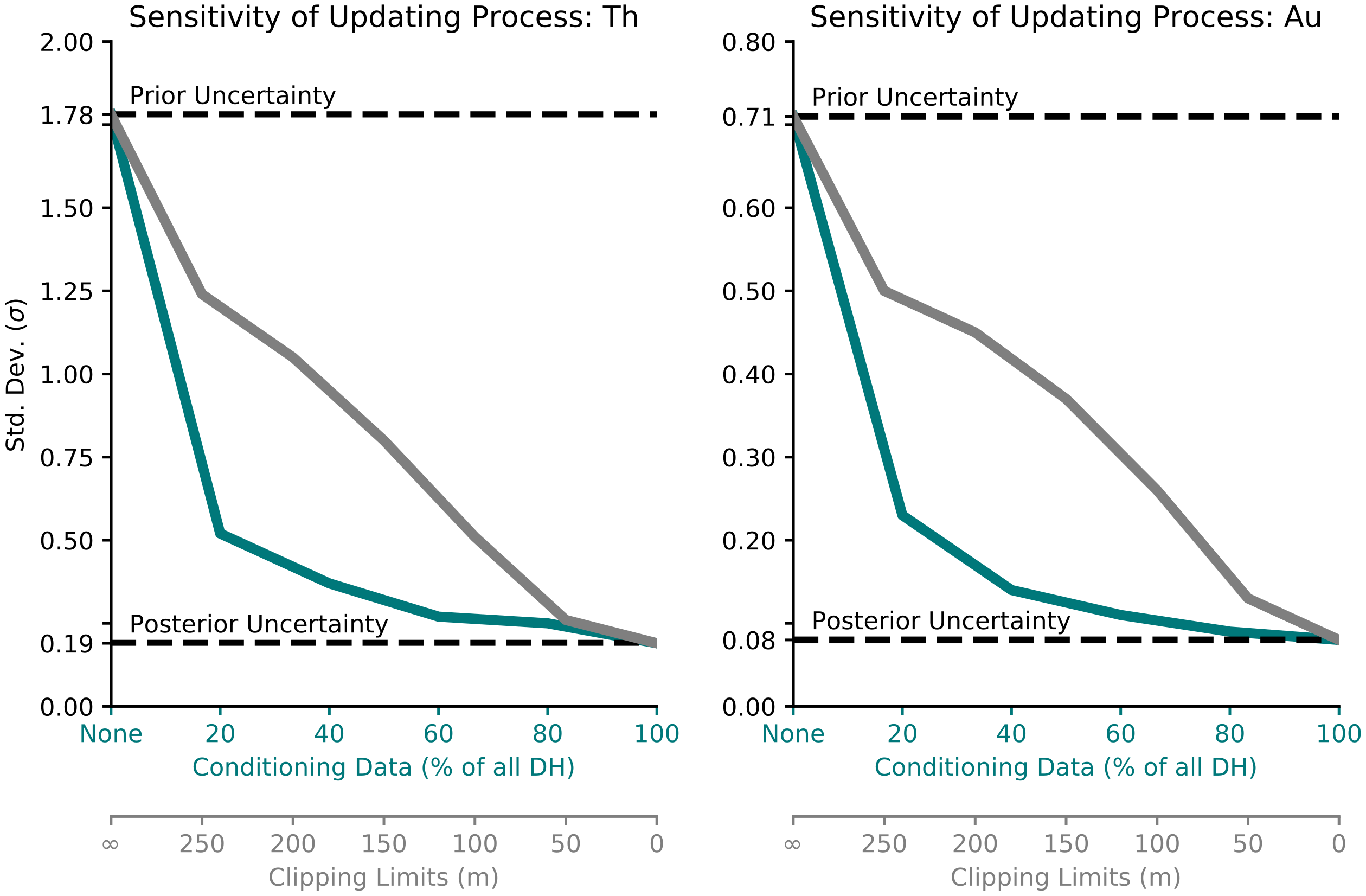
A sensitivity analysis is undertaken to illustrate the impact of independently modifying the number of conditioning data on the updating of the prior uncertainty distributions (Figure 7, green lines). Equal-sized subsets of the drill hole data were sequentially withdrawn from the original data to evaluate the impact of fewer available conditioning data. No other modifications are made to the workflow. Both \(Th\) and \(Au\) show a significant decrease in the standard deviation of the uncertainty distribution when using just 20% of the conditioning data in this example.

The effects of increasing the clipping limits in \(50m\) increments (Figure 7, gray lines) were less pronounced than the effects of the conditioning data. The greatest increase in the standard deviation occurs at \(250m\), which is the modeled range of the \(Th\) variogram.

Comparison to Simulation without the Multivariate Spatial Bootstrap

A subset comprising 80% of the data (\(n = 53\)) is generated to clearly highlight the difference between the posterior uncertainty distribution and the simulated uncertainty distribution without the multivariate spatial bootstrap (Figure 8). In comparison to the simulated \(Th\) uncertainty distribution, the standard deviation of the posterior uncertainty distribution increases 33% from \(\sigma = 0.24\) to \(\sigma = 0.32\). It is more pronounced for \(Au\), increasing 80% from \(\sigma = 0.10\) to \(\sigma = 0.18\).

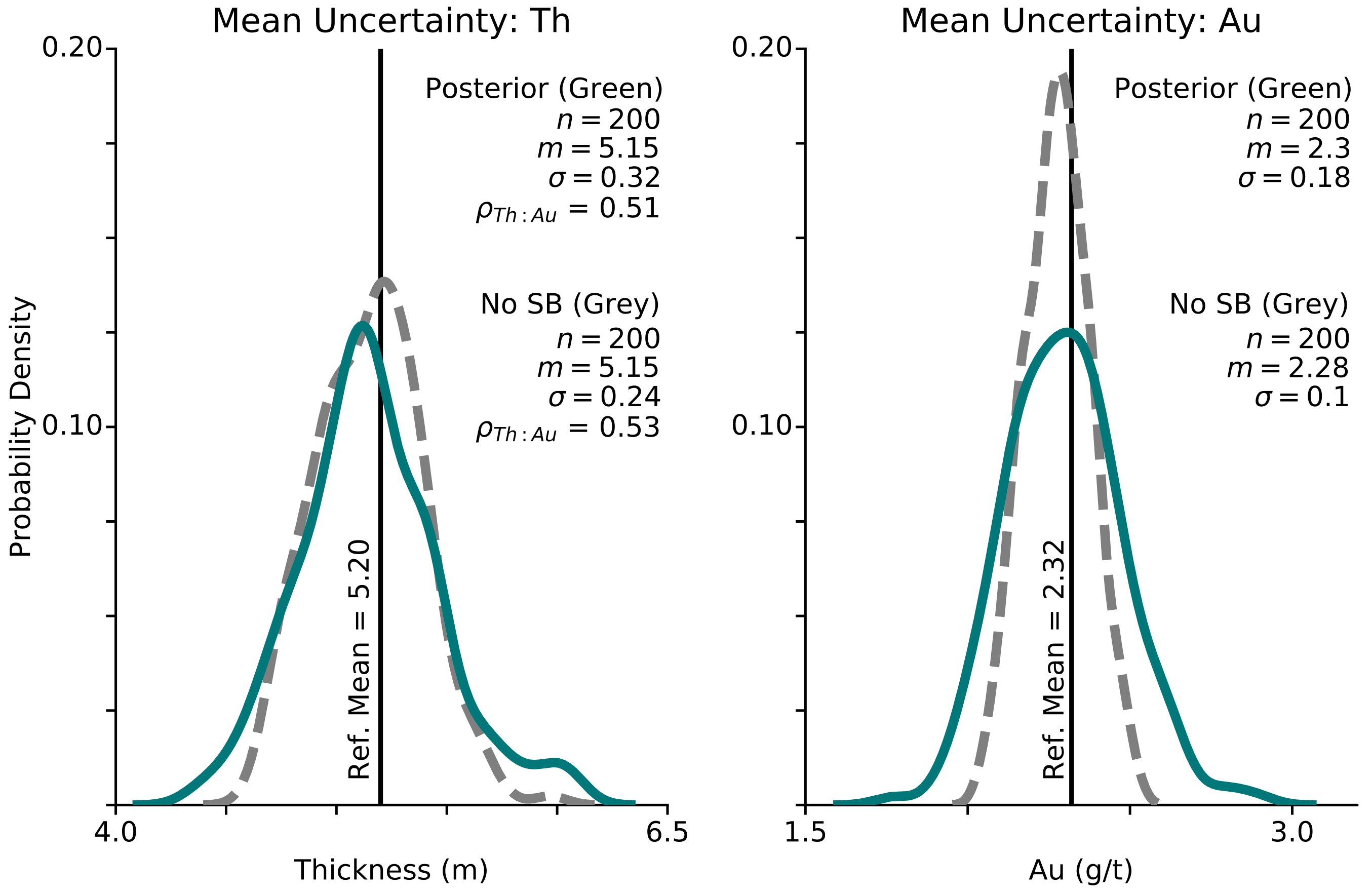
The input declustered mean (black line) matches closely the mean of each of the distributions. The correlation of \(Th\) and \(Au\) agree with the input correlation of \(\rho_{Th:Au} = 0.50\), which demonstrates the spatial relationship between the variables is respected.

Summary

Incorporation of the multivariate spatial bootstrap in the geostatistical workflow is used to improve uncertainty in mineral resources. The parameters of the global input histogram are primary factors controlling global uncertainty. Updating of the prior histogram uncertainty to the posterior histogram uncertainty is accomplished by (1) conditioning the spatial bootstrap realizations by the input data during simulation and (2) application of the domain clipping limits. This technique preserves the multivariate spatial relationships.

References