Learning Objectives

• Understand utility theory and risk preferences
• Understand the mean-variance criterion, efficient frontier and dominance
• Review loss functions

Introduction

Decision making is the process of selecting from a set of alternatives, the one that best satisfies our objectives. Bernoulli (1954) was a pioneer in this topic suggesting that our decisions should be based on a subjective internal representation of value or “utility” rather than pure monetary value. Others developed and extended the concept and applications of utility in decision making (Levy, 2016; Markowitz, 1959; Von Newmann & Morgenstern, 1944). Geological uncertainty entails that planned production may not be met or may be exceeded. The careful application of geostatistical and other numerical tools can lead to an accurate and precise characterization of geological uncertainty. The decision making process should consider this geological uncertainty. In some circumstances such as short term planning it is reasonable to be risk neutral. In other circumstances such as medium and long term planning we may want to be risk averse to mitigate against low outcomes. This Lesson is primarily aimed at reviewing the analysis tools that could be used for decision making in presence of geological uncertainty.

Risk is considered to be the negative consequences of a different outcome than expected in terms of economic performance. There are many other aspects of risk related to the environment, safety and society; however, our attention is on technical performance risk assuming these other risks are being taken seriously and managed appropriately. Our goal is to manage risk/opportunity caused by geological uncertainty. Achieving less than planned has a direct consequence in any mining or petroleum operation; achieving more than planned is less consequential, but it can leave a sense that the design could be conservative and sub-optimal.

Engineers often need to choose from a set of alternatives or optimize continuous variables. Alternative decisions have different outcomes. In some cases, the decisions are straightforward and simply maximizing expected value is sufficient. It is always desirable to avoid low outcomes and seek high outcomes, but the relative importance can change. The tools for this are well established - starting with utility theory.

Utility Theory

Before utility theory, there was a consensus that a rational decision is the one that maximizes the expected value from a set of alternatives. This approach does not yield meaningful results when outcome distributions share similar expected values or when the expected outcome becomes unacceptable to most decision makers due to unreasonable large results as described in the St. Petersburg paradox (Bernoulli, 1954), the latter paved the way for utility theory. There may be circumstances such as in exploration where investors value more the high outcomes and are less concerned about low outcomes. Whenever there is non-linearity in our perception of the value due to the presence of subjective risk attitudes, a utility function should be used instead of a value function (Bratvold & Begg, 2010). Unlike an expected value criterion, the utility theory introduced from economics is a consistent and comprehensive theory of risk (Cozzolino, 1977). The utility function is a subjective measure that encodes an individual’s preference. In utility theory, the or is a quantification of the individual decision maker’s value, therefore the utilities are relative to each decision maker’s preferences. The correct decision is the one that maximizes the expected utility (Von Newmann & Morgenstern, 1944).

Risk Preferences

In the Neumann-Morgenstern (1944) theory of utility, a risk neutral decision maker would not assign different relative values; an outcome with twice the value is twice as desirable. A risk averse decision maker is more sensitive to losses than gains of the same magnitude. An opportunity-seeking decision maker is attracted to the possibility of high outcomes (Levy, 2016).

The figure above shows two probability distributions (A and B) that have the same expected value, but different variance. These decisions are equal considering the expected value reasoning. In the utility framework a decision maker would prefer one of these alternatives based on their own utility function. Three utility functions are sketched to the right. A risk neutral decision maker has a linear utility function and is indifferent to choices with equal expected value even if one has a higher variance. A risk averse decision maker will penalize the risk related to lower valued outcomes with a concave down function; they would prefer A over B. An opportunity seeker looks for high outcomes or potential with a convex function, they would prefer B over A.

The utility function is subjective and depends on the individual and circumstances. The position may depend on the specific stage of a mining or petroleum project. As suggested above, mineral exploration may adopt an opportunity seeking stance since most deposits never make it to production. Only the very best ones are viable. In mine planning a risk averse stance is suitable since under performance would be more consequential than the good news of over performance. In day to day grade control decision making a risk neutral stance would likely be the best. Adopting a risk averse stance would avoid some low outcomes at the expense of lower expected profit. Adopting an opportunity seeking stance would avoid losing some high outcomes at the expense of a lower expected profit (Deutsch & Manchuk, 2018). Given the repetitive nature in grade control, a risk neutral position is recommended. Similar reasoning could be applied to different decision making contexts.

The Mean Variance Criterion

Explicitly defining the utility function is a challenge. The mean-variance criterion (MV) is a widely used approach for risk averse decisions especially in finance. The risk is described by the variance of the distribution of a response variable, that is, high variance means higher probability of low outcomes (Markowitz, 1959). The maximum value decision is taken for constant risk or, equivalently, the minimum variance decision is taken for constant value. The set of points that maximize value/minimize variance are referred to as the efficient frontier or Markowitz’s efficient frontier.

\[ E(F) \geq E(G) \mbox{ and } Var(F) \leq Var(G) \]

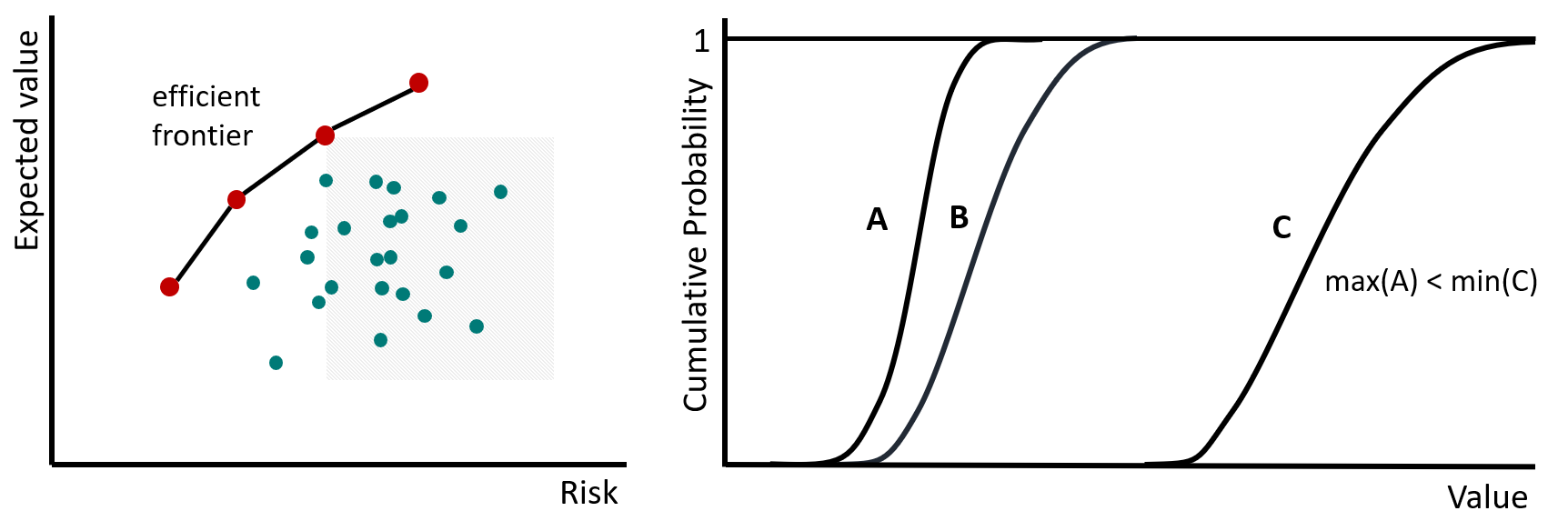
The sketch on the left of figure below illustrates this concept. Each point on the efficient frontier invalidates decisions that have lower value and higher risk (the gray box is an example). The concept is appealing. Depending on our degree of risk aversion, we may choose a lower valued decision with lower risk. However, not all points that appear to be on the efficient frontier are viable decisions. The concept of decision dominance is considered to eliminate some decisions.

Dominance

The sketch on the right of figure above illustrates the concepts of outcome and stochastic dominance. Alternative C outcome-dominates alternative A; the minimum outcome of C is greater than the maximum outcome from alternative A. Any rational decision maker would choose C. In other cases some alternatives can be stochastically dominated by others (Levy, 2016), for example, alternative A is stochastically dominated by alternative B if the outcome of A is less than the outcome of B for all cumulative probability values. Stochastic dominance requires that the cumulative distributions of alternatives being compared do not cross each other (Gallardo, 2019).

The MV criterion and Markowitz’s efficient frontier reduces the number of alternatives. The advantage of the analysis is to allow the decision makers to postpone their final subjective input until the end of the analysis (Cozzolino, 1977). Similarly, dominance rules further reduces the number of alternatives. The alternatives remaining on the efficient frontier after dominance rules must be chosen by judgement or an explicit utility function.

The mean-variance criterion can be adapted to treat risk under geological uncertainty. Gallardo (2019) shows an application that considers the mean-variance criterion and stochastic dominance to improve the decision-making in reservoir management. Acorn (2018) develops another application of MV to manage the risk/value trade-off for pit optimization.

Downside Risk

Risk may simply refer to the possibility of undesirable events going to happen. It originates from a situation involving uncertainty and relates to the future outcome. Markowitz (1959) put forward the mean-variance criterion in the portfolio selection, the risk is measured by the variance in this decision model. However, variance is often considered inadequate to assess risk in the mean variance criterion, as people are mainly concerned about the volatility below a certain level. Alternatives have been developed to improve the assessment of risk. Markowitz (2014) commented the semi-variance could be an alternative of variance in the measure of risk. Viole & Nawrocki (2013) claimed the risk in investment could be quantified by the probability of investment return below a specified benchmark. Klebaner et al (2017) used the lower partial moments to assess the downside volatility and quantify the risk. An application in oil industry decision making in drainage area design and surface pad is presented in Yang (2020). Given a random variable \(X\), the N-th lower partial moments are with respect to a truncated value \(x_{0}\).

\[ L P M_{N}\left(x, x_{0}\right)=(-1)^{N} \int_{-\infty}^{x}\left(x-x_{0}\right)^{N} d x \]

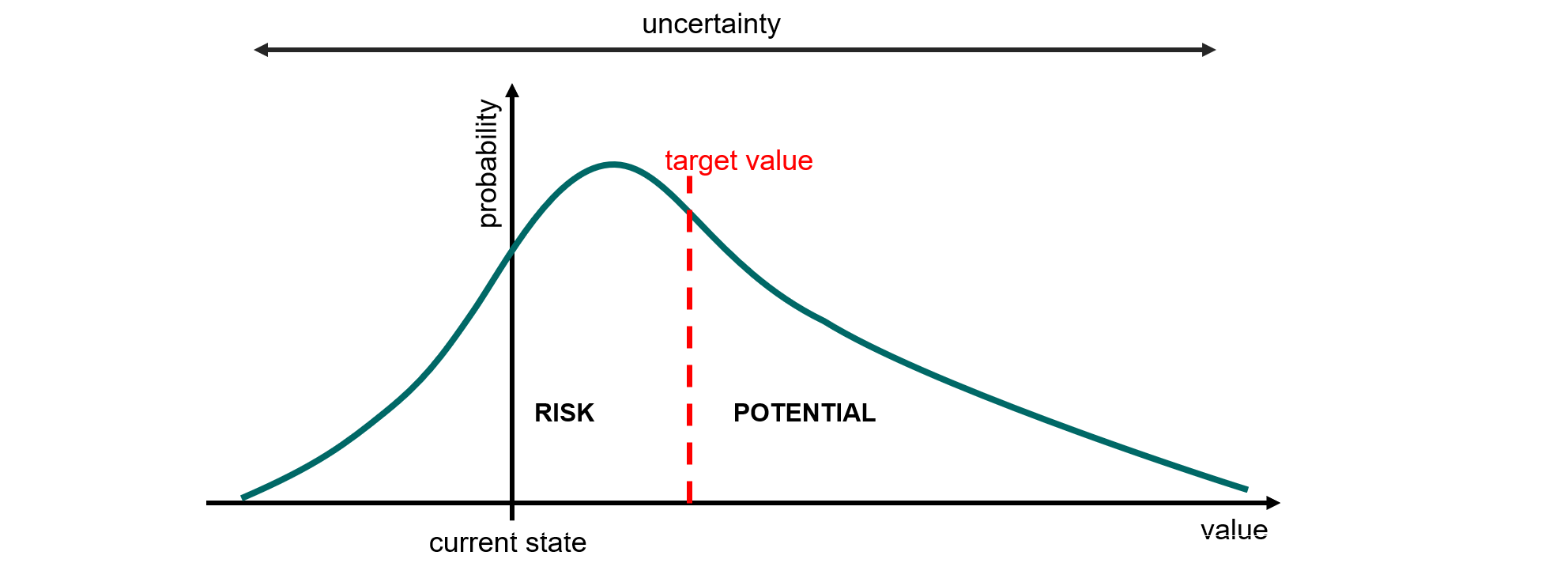
Downside risk, uncertainty and other components in a probability distribution are shown in the previous graph. The probability distribution is truncated to the risk and potential by a target value \(x_{0}\). In the upside-potential our utility function is opportunity-seeking; in the risk-side our attitude is risk-averse. Variance or standard deviation are commonly treated as the measure of uncertainty. Decision makers prefer lower risks and higher potentials, best decisions depend on analyzing the impact of different attitudes in the risk-potential sides.

Loss Function

Loss functions were considered in geostatistics before utility functions and the alternatives presented above (Journel, 1984). They did not gain widespread implementation because the purpose is more specific, that is, to choose a single value from a distribution \(F(z)\) that minimizes expected loss. Loss functions quantify the consequences \(L(e)\) for an error \(e=z^*-z\) where \(L\) is a specific and subjective loss function. The expected loss is computed for any estimate \(z^*\). The value that minimizes the expected loss will be retained as the optimal estimate. Loss functions can be case-specific or a conventional quadratic, linear or asymmetric linear function.

\[ \textit{ L-optimal } z^* = argmin_{z^{*}} \mbox{ }E\{L(z^*-Z)\} \]

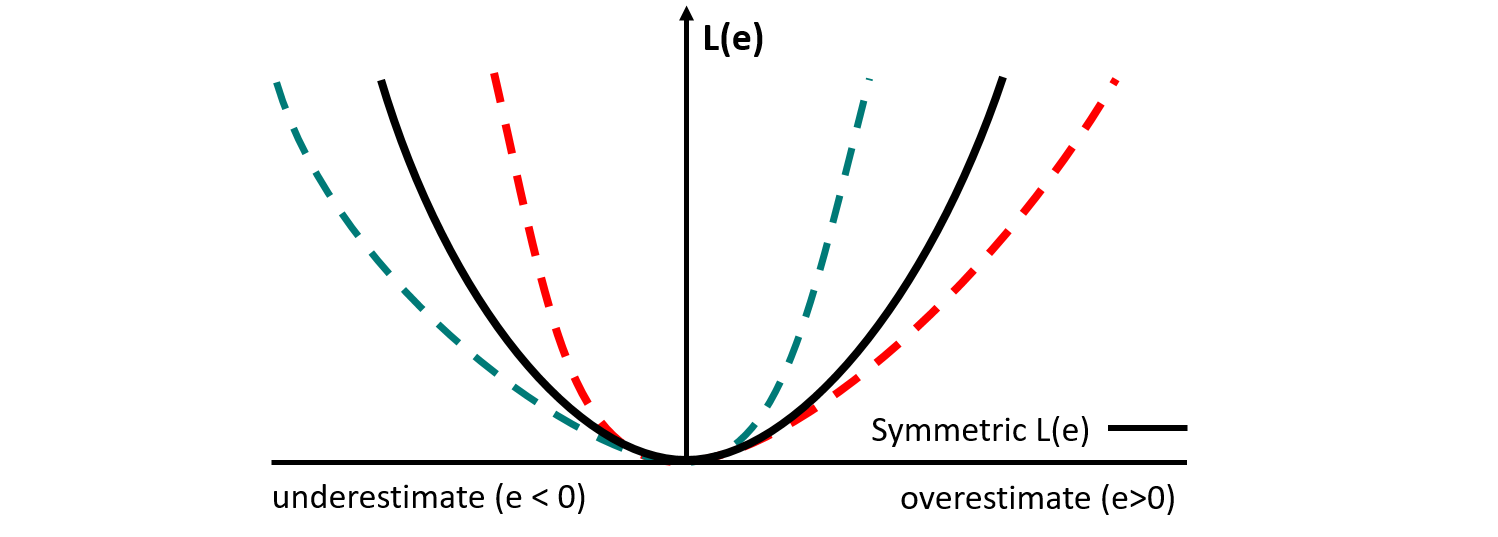
The loss function permits calculation of a best estimate from a distribution which is different than selecting an option from a list.

Example

For readers using a browser, the next figure (upper right) shows the uncertainty described by a parametric Gaussian distribution with mean 10 units and variance of 1.5, the bottom-left shows a quadratic loss function of the form \(L = e^2\) utilized to penalize the error, the bottom-right figure shows the expected loss value for every of the estimates retained. The correct choice \(z_{L}^*\) is the minimum value observed. Additionally, using the interactive slidebar we can go through different asymmetric loss functions, the resulting optimal estimate value is displayed as a vertical red line. A higher slope in the loss function for overestimation matches a risk-averse attitude, that is, we avoid specifying a too-high value.

Concluding Remarks

The purpose of this lesson is to briefly review and summarize the main tools for decision making. Considering straightforward expected value may be a reasonable approximation in many situations (Bratvold & Begg, 2010). Explicit consideration of risk requires an expected utility framework. In utility theory, the rational choice is to select the alternative with the largest possible utility. Once we have a model of uncertainty in all required parameters, decision making proceeds as follows: (1) define the objectives and a measurement scale either utility/profitability, (2) list all alternatives/courses of action, perhaps a decision-tree approach in some cases perhaps a continuous variable optimization on other cases, (3) calculate the expected utility for the available alternatives, (4) choose the alternative that maximizes the expected utility.

References