Learning Objectives

• Review the concept of support and the volume variance relation
• Demonstrate the importance of considering a change of support model when estimating recoverable resources
• Appreciate the additivity of variance and dispersion variance notation
• Understand the practical application of change of support models

Introduction

The data available for mineral resource estimation primarily comes from diamond drill core or reverse circulation (RC) cuttings. These data represent a small volume relative to the volume relevant for mining. The high and low values average together and the larger the support the less variable and more symmetric the distribution becomes (Isaaks & Srivastava, 1989). The data support distribution of an attribute will have greater variance than the block distribution of the same attribute (Rossi & Deutsch, 2013).

The change of support from composited drill hole data to a practical mining scale is important for the estimation of recoverable resources. A change of support model predicts how grade distributions change with volume support considering only data and statistics of the composited drill hole data.

Volume Support

The grade within mineral deposits is variable at all scales. A small diameter core sample could be high grade or low grade. As the volume or support of the core sample increases the observed variability will decrease and the distribution will become more symmetric. Most grade variables are mass fractions and scale linearly; therefore the mean does not change with support.

A selective mining unit (SMU) may be considered the smallest volume that a mining operation can select between ore and waste (Parker, 1980). Often, the SMU size is increased to account for imperfect information at the time of mining and other considerations. The SMU geometry depends on the mining method, equipment size and selectivity characteristics of the deposit. Open pit SMU sizes range from 5x5x5m for a highly selective operation to 20x20x15m for large bulk-tonnage porphyry deposits. The grade of an SMU can be thought of as an average of many smaller support samples such as drill hole composites.

A typical three meter long diamond drill core sample represents 5-25 kg of material while an open pit SMU may represent 325-20,000 tonnes of material. This 5 to 7 order of magnitude increase in support from the data and the SMU is an important consideration when estimating long term recoverable resources. The decrease in variance for a specified SMU size should be quantified. A hypothetical grade distribution is shown below. The black curve represents the distribution for the data support, the red curve with lesser variability represents a small SMU support, and the green curve with even less variance represents a larger SMU support. If the cutoff grade is above the mean grade, as in \(\mathbf{z}_{\mathbf{c2}}\), the estimated tonnage exceeding this grade will decrease as the support increases. If the cutoff is below the mean, as in \(\mathbf{z}_{\mathbf{c1}}\), the estimated tonnage above this cutoff increases as support increases. Anticipating the correct change of support is important for estimating resources at an SMU support.

Additivity of Variance

An important aspect of the volume variance relation is that variances are additive. Consider the following small example of eighteen small scale values \(v_i,i=1,...,18\) that define a domain \(A\) (the rectangular box):

\[ \begin{array}{|c c c c c c|} \hline 0.572 & 0.564 & 0.409 & 0.866 & 0.059 & 0.296 \\ 0.770 & 0.974 & 0.520 & 0.829 & 0.320 & 0.699 \\ 0.060 & 0.018 & 0.472 & 0.641 & 0.040 & 0.218 \\ \hline \end{array} \]

The mean and variance of all points within the domain is 0.463 and 0.088, respectively. If the data are grouped into three 3x2 blocks \(V_i,i=1,...,3\) we get the configuration below:

\[ \begin{array}{|cc|cc|cc|} \hline 0.572 & 0.564 & 0.409 & 0.866 & 0.059 & 0.296 \\ 0.770 & 0.974 & 0.520 & 0.829 & 0.320 & 0.699 \\ 0.060 & 0.018 & 0.472 & 0.641 & 0.040 & 0.218 \\ \hline \end{array} \]

\[ \begin{array}{|c|c|c|} \hline m_{V1} & m_{V2} & m_{V3} \\ 0.493 & 0.623 & 0.272 \\ \hline \end{array} \]

The variance of points within the blocks is: \[Var(v_i,V_1)=\frac{1}{6}\sum_{i=1}^6(z_{vi}-m_{V1})^2=0.122\]

\[Var(v_i,V_2)=\frac{1}{6}\sum_{i=1}^6(z_{vi}-m_{V2})^2=0.030\]

\[Var(v_i,V_3)=\frac{1}{6}\sum_{i=1}^6(z_{vi}-m_{V3})^2=0.048\]

\[Var(v,V)=\frac{1}{3}(0.122+0.030+0.048)=0.067\]

And the variance of blocks within the domain is: \[Var(V,A)=\frac{1}{3}\sum_{i=1}^3(m_{Vi}-m_A)^2=0.021\]

The sum of the variance of the components equals the total variance of the data: \[\begin{aligned} Var(v,A) &= Var(v,V) + Var(V,A) \\ 0.088 &= 0.067 + 0.021 \\ \end{aligned}\]

The variance of points in the domain is the average or expected variance of points in the blocks plus the variance of blocks in the domain. This does not depend on any statistical assumptions such as stationarity.

Dispersion Variance Notation

The variance of a distribution with respect to its support is characterized by the dispersion variance notation \(D^2(v,V)\) where \(v\) represents a small support of the values, and \(V\) represents a larger support of the mean. This is the variability of the data of smaller support within the larger volume.

As shown above, the total variance in a domain \(A\) is equal to the sum of the average variance of points within blocks of some volume \(V\) and the variance of those blocks within the domain \(A\) (Isaaks & Srivastava, 1989):

\[D^2(v,A)=D^2(v,V)+D^2(V,A)\]

This relationship is known as Krige’s Relation. As we are interested in the dispersion variance of blocks \(V\) within some domain \(A\), we re-arrange the above equation to:

\[D^2(V,A)=D^2(v,A)-D^2(v,V)\]

The dispersion variance of the data within the domain is equal to the sample variance, \(D^2(v,A)=\sigma^2\), and the dispersion variance of point data within the block, \(D^2(v,V)\), can be calculated from the variogram model.

Average Variogram Values: “Gammabar”

The average variogram value within a volume \(V\) is denoted \(\overline{\gamma}(V,V)\) and calculated as the average variogram value for all possible pairs where both ends of the vector are in the volume:

\[\overline{\gamma}\left(V,V\right) = \frac{1}{V \cdot V} \int_{V} \int_{V} \gamma(y-y') dy dy' \approx \frac{1}{n \cdot n} \sum_{i=1}^n \sum_{j=1}^{n} \gamma({\mathbf u}_i - {\mathbf u}_j)\]

The integral is approximated as a discrete sum for convenience. Consideration must be given to the number of discretization points to achieve a stable result. A 5x5x5 discretization is considered sufficient to provide a reliable estimate of the average variogram (Isaaks & Srivastava, 1989); however, further consideration must be given to the number of discretization points in the direction of drilling. If the composite length matches the SMU dimension discretization in the \(z\) direction should be set to one to avoid artificially increasing the average variogram. If the composite length is half the SMU dimension the discretization should be two.

SMU support also influences the average variogram value. As the block size increases the average variogram value increases and the block support variance must decrease.

The variance correction factor (VCF), or \(f\), is commonly defined as the ratio of block variance to sample variance:

\[f = \frac{D^2(V,A)}{D^2(v,A)} = \frac{\sigma^2-\overline{\gamma}\left(V,V\right) }{\sigma^2}=1-\frac{\overline{\gamma}\left(V,V\right)}{\sigma^2}\]

The VCF can provide an indication of the impact of the change of support. An \(f\) close to one suggests the two variances are similar either due to a highly selective SMU size or geologic continuity; little mixing of material will occur (Rossi & Deutsch, 2013). A small \(f\) value indicates the opposite and there will be a significant change in variance and resources above cutoff, at the selected SMU scale.

Change of Shape

The shape of the distribution will change as support increases. The central limit theorem tells us that the distribution will converge to the Gaussian distribution as support increases. An important factor contributing to the change in shape is the geologic continuity of the variable in question. Highly continuous deposits will experience a less drastic mixing of highs and lows when the data is scaled up. Grade distributions of highly structured or discontinuous deposits may experience significant changes of shape as the data is scaled up.

The following dynamic figure illustrates how an up-scaled distribution of copper changes as a function of the variogram. The block scale is 15x15x15m and light gray curve is the original drill hole data. Note as the continuity of the variable decreases the distributions become increasingly low variance and converge to the mean value.

Variograms and corresponding block distributions. Use the slider at the bottom to step through varying measures of spatial continuity.

Change of Support Models

The variance reduction from data to an SMU is known from the average variogram. A change of shape model is necessary to accurately predict recoverable resources. As the data is scaled up the distribution will become progressively more Gaussian in shape. By correcting the data distribution to the SMU support distribution prior to estimation, the practitioner has a target distribution for the estimated model (Rossi & Deutsch, 2013). With all change of support models, the distribution of SMU grades maintains the same mean while the variance is reduced by the variance correction factor from the average variogram.

Historical Change of Support Models

The following change of support models are not recommended due to the strong assumptions required (Rossi & Deutsch, 2013). Details of the methods are discussed in the geostatistical literature (Chilès & Delfiner, 2009; Isaaks & Srivastava, 1989; Journel & Huijbregts, 1978).

The affine correction reduces the variance of the distribution without changing its shape. This assumption of the permanence of shape is limiting as artificial minimum and maximum values are introduced and we know the distribution will become more symmetric as the support increases. It would only be correct for a distribution which is Gaussian at the smallest scale.

The indirect log normal correction assumes the point and block distributions are both log-normal with the same mean and different variances (Isaaks & Srivastava, 1989). A quantile-quantile transformation from one distribution to the other is performed; however, the mean is not preserved if the distributions are not exactly log-normal. A second step of rescaling the values to the correct mean is required. Although better than the affine correction, the shape change is unrealistic.

Discrete Gaussian Model

The discrete Gaussian model (DGM) is considered a more robust change of shape model than those mentioned above as it makes more reasonable assumptions. The DGM works on a Gaussian transform of the original variable. The relationship between original grades, \(Z\), and the normal scores, \(Y\), is fit with a series of Hermite polynomials. The variance reduction is performed by scaling the coefficients by a change of support factor related to the variance reduction (Rossi & Deutsch, 2013). Details regarding the fitting of Hermite polynomials are presented by Chilès & Delfiner (2009) and Machuca-Mory, Babak, & Deutsch (2008).

The DGM requires an anamorphosis function to be fit. The function is defined by Hermite polynomial expansion up to order \(n_p\), where the distribution of the transformed data is (Machuca-Mory et al., 2008):

\[z(\mathbf{u})=\sum_{p=0}^{n_p}\phi_pH_p(y(\mathbf{u}))\]

Where \(\phi_p\) is the \(p\)-order polynomial coefficient and \(H_p(y(\mathbf{u}))\) is the \(p\)-order Hermite polynomial; \(n_p\) is typically set to 100. The distribution of SMU scale grades can then be determined by scaling the anamorphosis function by a support coefficient \(r\):

\[z_V(\mathbf{u})=\sum_{p=0}^{n_p}(\phi_pr_v)^{\omega}H_p(y(\mathbf{u}))\]

Where \(r_v\) is chosen such that the variance of the block values matches that predicted above and \(\omega\) is a measure of dissemination which is typically chosen as \(p\) for disseminated deposits and 1 for highly structured deposits.

Practical Applications of Change of Support Models

A change of support model is useful when evaluating recoverable resources. It can provide a target for an estimated grade distribution, an indication of the degree of averaging that may occur and potentially highlight the importance (or not) of mining selectivity. The practical application of change of support models include the following.

Long Range Recoverable Resources

Due to the spatial variability of ore deposits, one cannot realistically recover all of the estimated “in-situ” resource. Out of the in-situ resource, only a certain portion will be selected as ore based on varying economic and technical considerations. Correctly estimating the recoverable proportion of material above this cutoff grade is of unquestionable importance when evaluating the viability of a mining project.

A recoverable resource model is one that takes into consideration aspects of the mining operation to quantify dilution that may affect the proportion of material above a defined cutoff grade. In practice, geologic contact and operational dilution must also be considered as well as internal dilution as a result of the SMU support.

Using an appropriate change of support model, the resource modeler can anticipate the expected distribution of grades at the SMU scale. This histogram can then be used to calibrate estimation parameters. All kriged estimates will be smooth, but one may employ a restricted search in an effort to control the degree of smoothing for an interim estimate. By restricting the total number of data used for the estimate, the modeler can target the expected distribution from the change of support model, particularly above a cutoff of interest.

One limitation of change of support models is that only internal dilution is considered. The distribution of estimated grades should not match the change of support distribution exactly as additional, site specific, geologic and operational dilution should also be considered.

Selectivity Analysis

Change of support models may also be used to assess the value of selectivity. This assessment would be based on the impact that various sizes of mining equipment, and thus various SMU sizes, would have on dilution for the given operation. This is typically done by comparing SMUs of varying size as shown below:

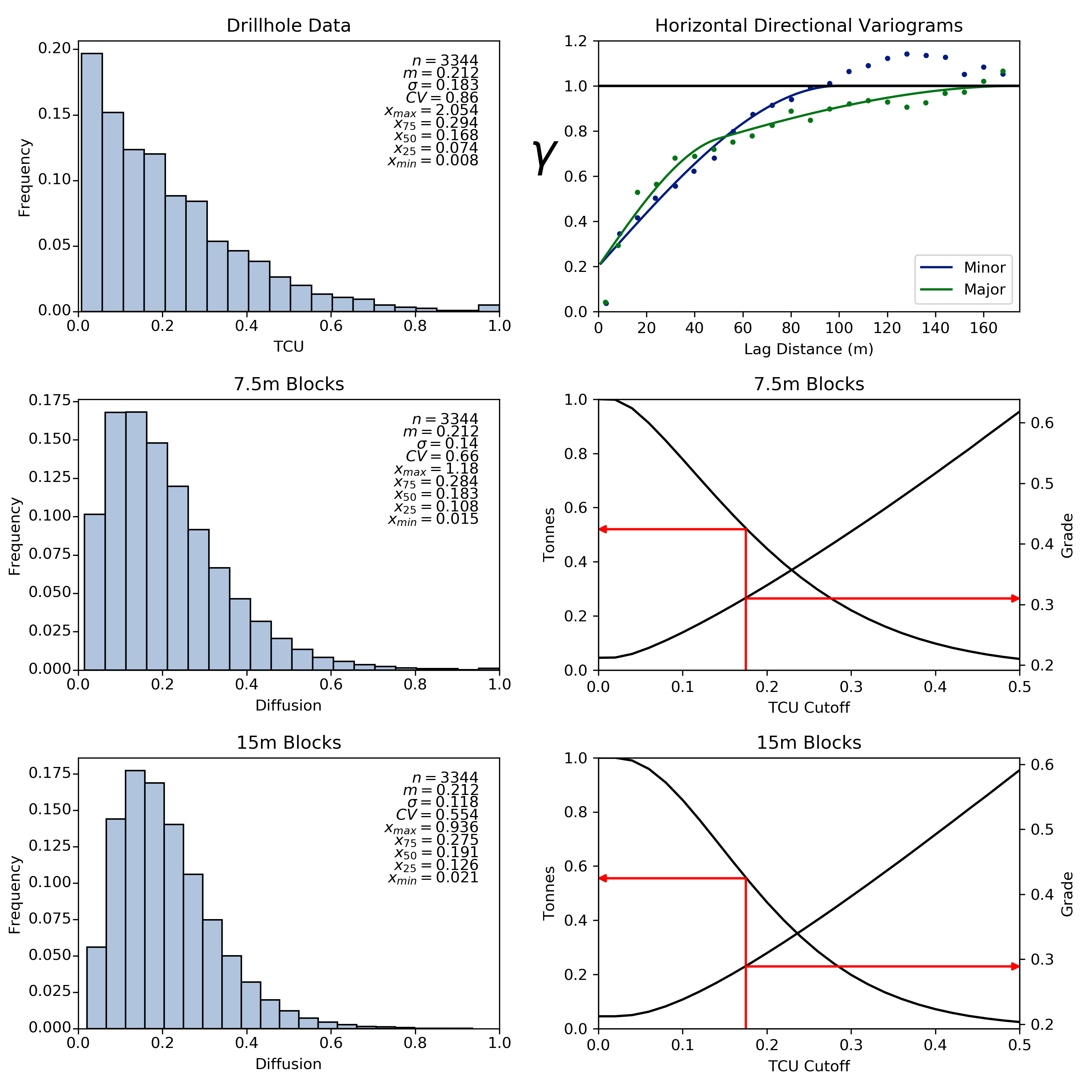
The histogram of the drill hole data is scaled to the two block supports using the illustrated variogram model and the discrete Gaussian change of support model. Note the change in shape of the histogram as the support increases - the variance decreases, the maximum value decreases, the minimum value increases and the distributions become more symmetric. The data and variogram are the same for both grade tonnage curves, only the support has changed. The 0.175% Cu cutoff grade is below the mean in this example. 7.5m blocks yield 52% of the total tonnage above cutoff at a grade of 0.310% Cu while 15m blocks yield 56% of total tonnage above cutoff at a grade of 0.289% Cu.

The value of the recoverable resource for a given selectivity is compared to the operational cost of achieving such selectivity. This investigation may provide justification for split benching (ie. 7.5m vs 15m benches) or the use of a hydraulic excavator near ore-waste contacts. One drawback of using change of support models for selectivity analysis is the assumption of free and perfect selection. Mining at contacts may be more selective than the SMU size or conversely an isolated pod of ore within a substantial volume of waste will likely not be recovered.

Summary

Understanding how a grade distribution will change as it is scaled up to a larger support is a critical component of assessing recoverable resources. Krige’s Relation and the additivity of variances tells us how variance changes with support. A direct relationship exists between the point support variance, the variance of points within the SMU volume and the variance of the SMU volume within the domain. The average variogram, \(\overline{\gamma}(V,V)\), is the expected variance of points inside a volume \(V\) and can be calculated from the variogram model and the SMU geometry. The geologic continuity of the variable has a significant impact on how the shape of the distribution will change. The DGM provides a robust change of shape model. The volume variance relation can provide the grade distribution representative of what will be mined. This provides a target for estimation of recoverable reserves.

References