Learning Objectives

• Explain the definition of key tolerance parameters required for 3D experimental variogram calculation in irregularly sampled data sets
• Specify reasonable experimental variogram tolerance parameters including lag distances and tolerances, angles, and bandwidths
• Check an experimental variogram for conformance to geologic interpretation and suitability for modeling

Introduction

The variogram is a central parameter for many geostatistical techniques. Kriging, Gaussian simulation, and indicator methods all require a variogram model for each variable in each domain. The definition and calculation of the variogram is covered in any standard geostatistical text (Chilès & Delfiner, 2009; Pyrcz & Deutsch, 2014). This lesson focuses on variogram calculation in practical cases where the variogram must be inferred from limited, irregularly spaced measurements. In these cases, tolerance parameters are required to infer an experimental variogram that is both precise and stable for subsequent modeling.

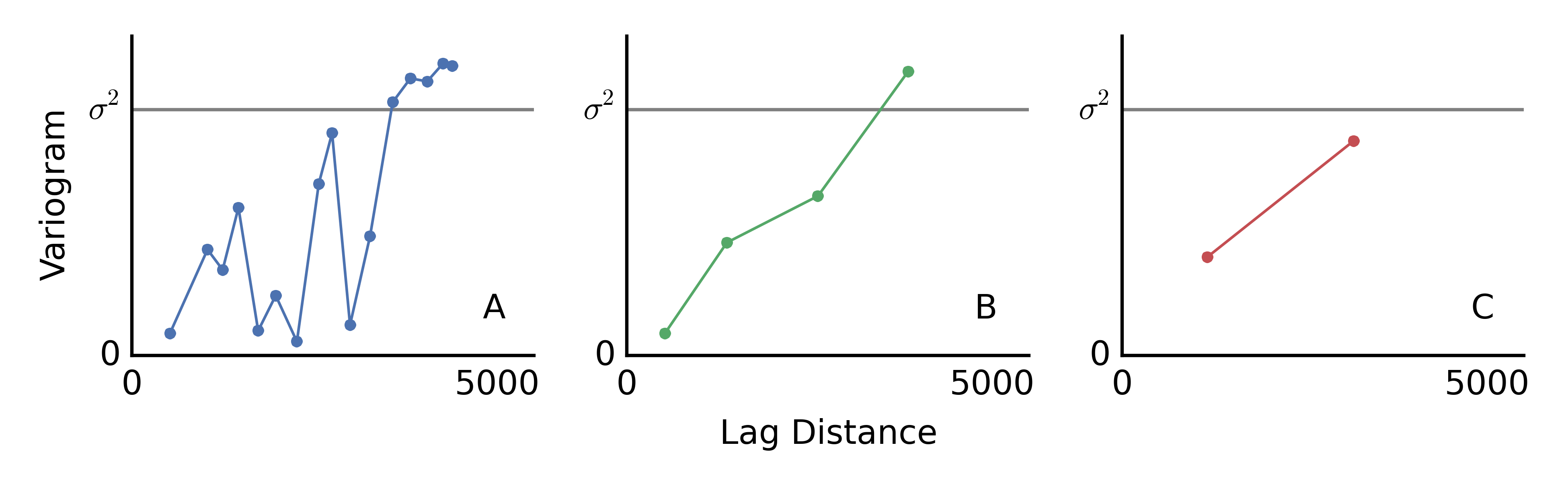
The trade-off between stability and precision is illustrated in the experimental variograms shown below. We consider variogram A to be overly precise and highly unstable with few pairs informing each point, and variogram C to be too imprecise for accurate modeling. This lesson provides a starting point for experimental variogram tolerance parameter selection with the goal of inferring a precise, stable variogram, such as variogram B.

Prerequisites

Prior to experimental variogram calculation, a number of prerequisites must be satisfied. The coordinates of the domain may be transformed to conform to the directions of continuity. Tabular deposits are almost always flattened or unfolded. A review of coordinate transforms and considerations specific to tabular deposits are discussed in a separate lesson (J. L. Deutsch, 2015).

Data compositing and extreme value management is required prior to variogram calculation. Data are typically composited to the largest reasonable length before any modeling operations (Rossi & Deutsch, 2013). Compositing to a larger scale substantially increases the stability of the calculated experimental variograms. The composited values may be transformed using a normal score transform (probit) or additional transform to manage extreme values.

Parameter Selection

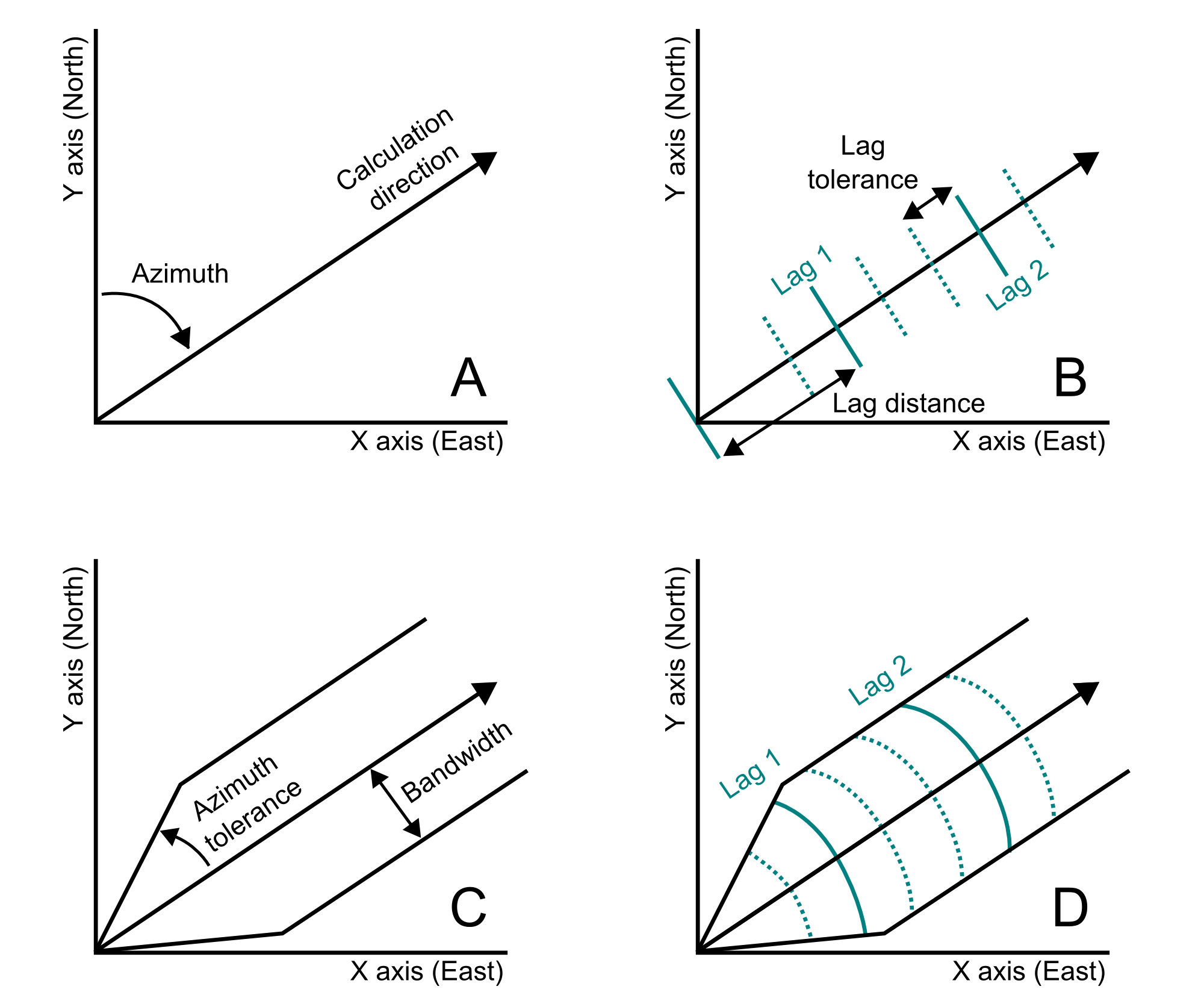
After any required coordinate and data transformation steps, the variogram is calculated in each principal direction. A direction is defined by azimuth and dip angles considering the area geology (A). A tilt may also be incorporated to rotate the tolerance parameters about the calculation direction axis. Lag parameters, including the lag spacing and tolerance, are chosen considering the size of the domain and data spacing (B). Angle tolerances and bandwidths consider variability in calculation directions and the sampling configuration (C). The final variogram tolerance definition includes all of these parameters (D).

Choice of Directions

Natural processes do not lead to isotropic spatial distributions. Typically there is a plane of major continuity, such as a vein or stratigraphic surface, and a direction of minimum continuity perpendicular to the plane. For a 3D data set, 3 orthogonal directions are required for experimental variogram calculation. These directions may be referred to as the major, minor, and vertical directions (C. V. Deutsch & Journel, 1998). The “vertical” direction is taken to be the direction orthogonal to the major plane of continuity composed of the minor and major directions; there is no requirement that the vertical direction correspond to the Z axis.

The 3 orthogonal directions are best chosen considering the natural process responsible for the variable, and area geology. The choice of direction may be chosen using geologic understanding together with visual inspection of the data. In the absence of strong geologic evidence for the orthogonal directions, a neutral model or variogram map is considered. A neutral model is constructed using a global (or very large search) estimation technique with an isotropic weighting function. Using ordinary kriging, the neutral model would be constructed with an isotropic, long range, high nugget effect variogram. Alternatively, an isotropic inverse distance model could be used. If a very large number of samples are available, a variogram map may be used to assist in the selection of directions. However, in many situations where the dense sampling required for a reasonable variogram map is available, the principal directions are already well known. Multiple methods of choosing directions may be combined; a neutral map and geologic understanding are often used together.

Choice of Lag Spacing

Lag spacing is chosen equal to the data spacing aligned with the direction of the experimental variogram. The lag spacing is likely to be different for each direction, as data are much more closely spacing along a drill hole. In sparsely sampled domains where multiple data spacings are present, multiple lag spacings may be used. That is, a variogram may be calculated with a lag spacing of 75 m for the first few lags, and a spacing of 500 m for a set of additional lags.

The choice of the number of lags to calculate is tied to the choice of lag spacing. The number of lags to calculate is conservatively chosen such that the calculated experimental variogram spans less than half of the domain size (Journel & Huijbregts, 1978). Calculating more lags results in pairing samples from the edges of the domain with each other. These variogram points will be much less informed than shorter distance points, with fewer pairs supporting the calculation.

Lag Tolerance

The lag tolerance is typically chosen to be equal to half of the lag spacing. If there are few data, then a larger tolerance may be required that results in overlapping tolerance bins and a more stable variogram. Dense sampling, or very regular sampling permits may permit a smaller lag tolerance.

Angle Tolerances

In the simple 2D sketch of a variogram tolerance definition shown earlier, only an azimuth angle tolerance is drawn. In addition to an azimuth angle tolerance, a dip angle tolerance is required for a 3D deposit. Both the azimuth and dip angle tolerances should be chosen such that a maximum reasonable number of pairs are found in the variogram search and unreasonable associations are limited. A common selection procedure is to choose azimuth and dip tolerances if 22.5° corresponding to a 45° span for points being considered. Based on experimental variograms calculated with these tolerances, the decision is made to reduce the angle tolerance, increasing precision, or increase the angle tolerance, increasing stability. Additional considerations are required when selecting angle tolerances for tabular deposits; the dip angle tolerance must typically be restricted for the horizontal variograms in these cases.

Choosing angle tolerances for the vertical variogram follow the same guidelines, although keeping in mind that the dip tolerance and azimuth tolerance are interchangeable for a perfectly vertical variogram. Recall that when setting angle tolerances in many geostatistical software packages, the angle tolerances are set to 90° for an omnidirectional variogram.

Bandwidths

As with angle tolerances, bandwidths are used to limit the number of unreasonable associations and maximize the number of reasonable pairs. In disseminated deposits, bandwidths are infrequently used as they seldom improve the stability of the calculated variogram. Instead, a carefully chosen set of angle tolerances (azimuth and dip) are applied. In tabular environments bandwidths are used to limit the number of pairs which geologic units (J. L. Deutsch, 2015).

The application of bandwidths varies among geostatistical software packages. GSLIB and related packages use a rectangular pyramid for clipping the experimental variogram. Many packages use an elliptic cone. In almost all situations, the difference in the resulting variograms is minor.

Criteria for a Reasonable Experimental Variogram

Using the experimental variogram tolerances, directional variograms are calculated and plotted. These are evaluated against a set of criteria for a reasonable experimental variogram. The experimental variogram should not be excessively noisy; recall the first figure in this lesson depicting an overly precise, but noisy variogram. The variograms should show structure; that is, there should be a degree of spatial correlation for a physical process. If the entire experimental variogram is at the sill, then this implies that there is no spatial correlation. This is unlikely for a variable which is controlled by a natural process. Finally, the experimental variograms should be consistent with our geologic interpretation.

Tolerances parameters discussed were applied for the calculation of experimental variograms using thickness-composited measurements of porosity at a Texas reservoir. This reservoir exhibits very strong continuity in the North-South direction, and limited continuity in the East-West direction. Experimental variograms in the North-South and East-West were calculated with a lag distance of 1200 ft which is approximately the data spacing over much of the reservoir. A lag tolerance equal to half of the lag spacing (600 ft) was chosen. Only 4 lags were calculated so that the variogram spans approximately half of the domain size. An azimuth tolerance of 12.5° was used with no horizontal bandwidth.

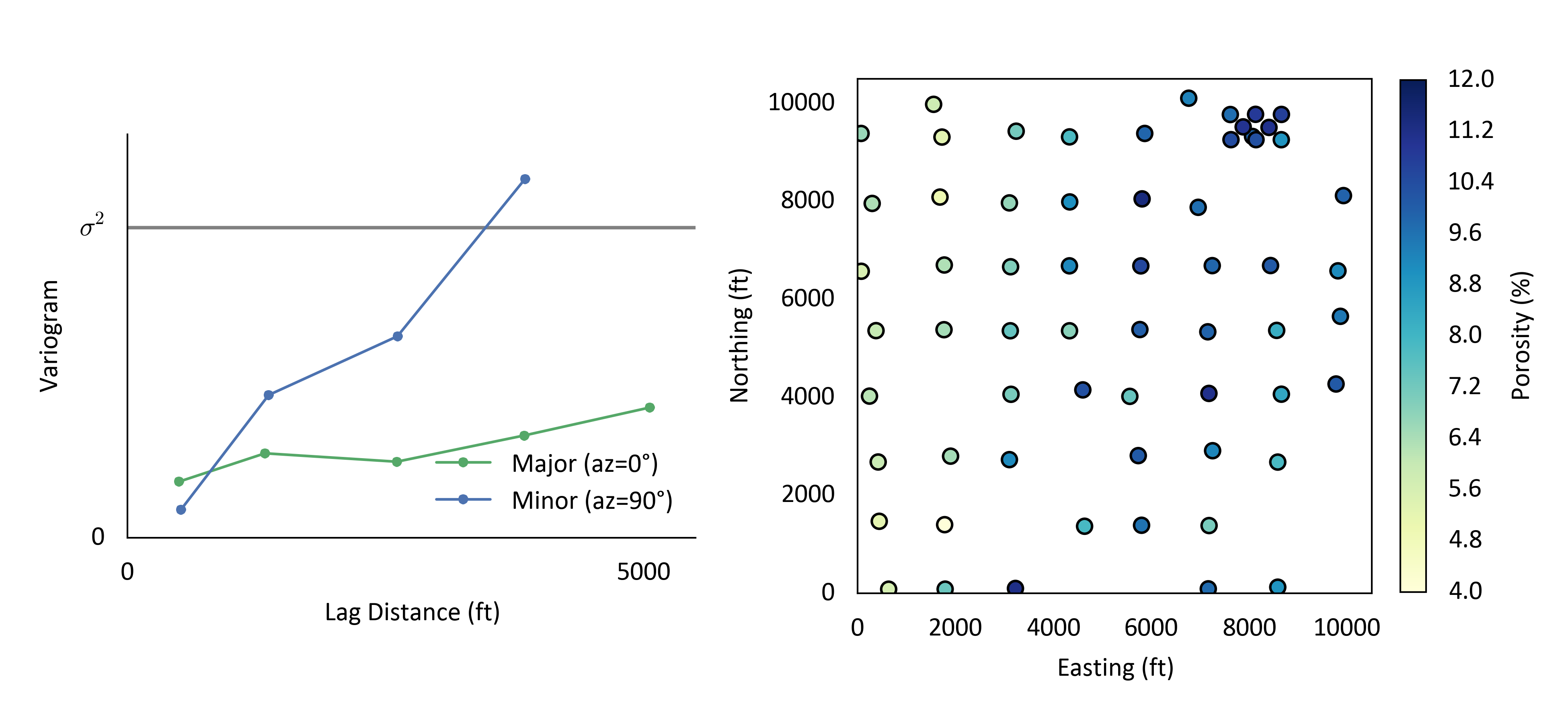
These variograms may be evaluated against the criteria discussed. The experimental variograms show structure, are not overly noisy and are consistent with the data exhibiting a strong zonal anisotropy.

Summary

There are many variogram tolerance parameters. Guidelines for selecting these tolerance parameters have been outlined in this lesson, but it is not possible to consider all geologic environments. Any variogram calculation parameters chosen poorly makes the variogram worse, that is, noisy, inconsistent with the geology and/or lacking structure. Experimental variograms should always be evaluated against these criteria to ensure the reasonableness of the experimental variogram.

References