Learning Objectives

• Understand the concept of Bayesian Updating and its application in spatial prediction.
• Explain the steps in Bayesian Updating for incorporating secondary variable(s) in the prediction of a sparsely-sampled primary variable.
• Review the derivation of the Bayesian Updating equations.

Introduction

In many geoscience disciplines, the main variable of interest is sparsely sampled. In many cases, complimentary secondary information from geophysics is incorporated into the modeling of the primary attribute of interest. As the secondary information is remotely sensed, much larger volumes can be sampled. Provided that there is sufficient linear correlation, these different types of data can be merged through Bayesian Updating to model the primary attribute of interest. In mining, widely-spaced borehole data in lateritic bauxite and nickel deposits may be supplemented by a ground penetrating radar survey. Similarly, in petroleum, reservoir quality measurements from widely-spaced wells can be supplemented by seismic data. In addition, multivariate data imputation (or assignment) for missing values often requires combining distributions from spatial data and collocated multivariate data.

Multivariate geostatistical approaches such as cokriging (Doyen, 1988) and collocated cokriging (Xu, Tran, Srivastava, & Journel, 1992) can be used to incorporate the exhaustive (available at all grid nodes to be predicted) secondary variable into the spatial prediction of the primary variable of interest. However, when there are multiple secondary variables, fitting a linear model of coregionalization could be tedious and restrictive. In Bayesian Updating, the only model requirement is the covariance of the primary variable which is required in any case (Deutsch & Zanon, 2004; Neufeld & Deutsch, 2004). This lesson aims at explaining with mathematical derivation how multiple secondary variables could be merged to predict a primary variable of interest through Bayesian Updating.

Consider that in the domain \(A\), there are two types of data available: (1) primary, and (2) secondary. The former (i.e. well or borehole data) is generally sampled sparsely, and the latter (i.e. the data acquired by a geophysical survey) provides non-invasive exhaustive information related to the primary attribute. The primary variable \(Y\) has been sampled at \(n\) locations, \(\{y(\textbf{u}_{i}), i = 1, \ldots,n\}\), and the secondary variables, \(\textbf{X}=[X_{1},\ldots,X_{m}]\) are available at \(N\) grid nodes within \(A\), \(\{x_j(\textbf{u}_{i}), \;j=1,\ldots,m,\; i=1,\ldots,N\}\) where \(m\) is the number of secondary variables and \(N\) is the number of grid nodes. Both primary and secondary variables are normal score transformed, \(Y, \mathbf{X}\sim N(0,1)\) and assumed multivariate Gaussian. The primary variable \(Y\) is assumed to be second-order stationary within the domain \(A\), \(E\{Y(\textbf{u})\}=0, Var\{Y(\textbf{u})\}=1, \forall \textbf{u} \in A\). The primary and secondary variables are merged through Bayesian Updating to predict the values of the primary variable at the unsampled location within \(A\) (Figure 1). The variance map for secondary data is constant in the domain, because the correlations are calculated using the data at the collocated locations and we assume they are constant in the domain, so the resulting variance is constant as well.

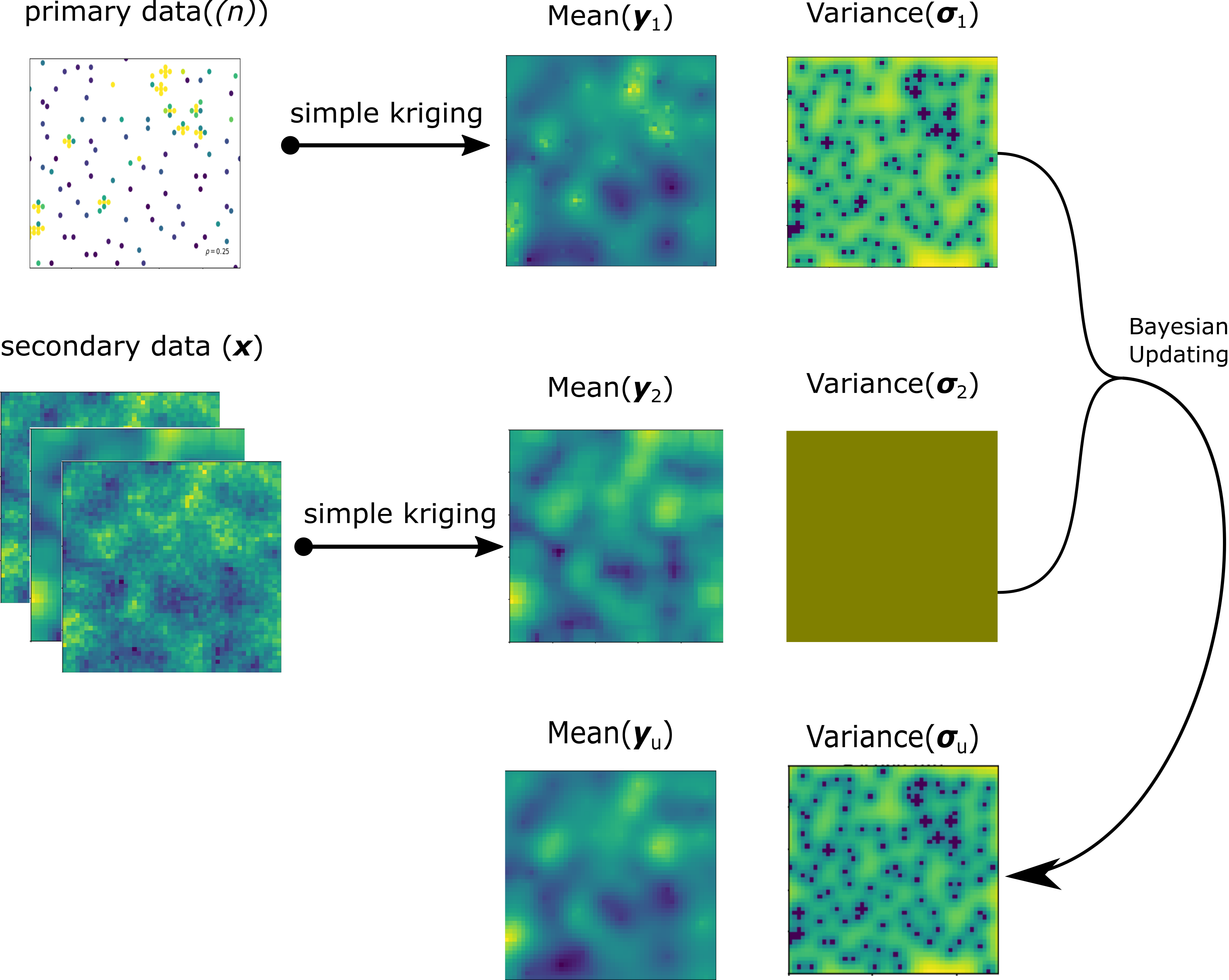
Consider a location \(\mathbf{u}_{}\) where the value of the primary variable is to be predicted. In Bayesian Updating, the primary data \(\{y(\textbf{u}_{i}), i = 1, \ldots,n\}\) which are not present at location \(\mathbf{u}_{}\), and the secondary data \(\{x_j(\textbf{u}_{i}), \;j=1,\ldots,m,\; i=1,\ldots,N\}\) which are present in the entire domain, are used for the conditioning. The steps are reviewed, then the mathematical derivation is given.

Steps of Bayesian Updating

Step 1

Calculate the mean \(\bar{y}_1 (\mathbf{u}_{})\) and the variance \(\sigma_1^2(\mathbf{u}_{})\) for the unsampled location \(\mathbf{u}\) conditioning to primary data \(\{y(\textbf{u}_{i}), i = 1, \ldots,n\}\) through the normal equations. It is noted that simple kriging is equivalent to normal equations in Gaussian units:

\[\label{sp} \begin{split} &\bar{y}_1 (\mathbf{u}_{})= \sum_{i=1}^{n} \lambda_i y(\mathbf{u}_{i}) \\ &\sigma_1^2(\mathbf{u}_{})= 1 - \sum_{i=1}^{n} \lambda_i C(\mathbf{u}_{}- \mathbf{u}_{i})\\ &\sum_{i=1}^{n} \lambda_i C(\mathbf{u}_{i}-\mathbf{u}_{k}) = C(\mathbf{u}_{}- \mathbf{u}_{k}), \;\; k=1,\ldots,n \end{split}\]

\(C(\mathbf{u}_{i}- \mathbf{u}_{k})\) are the data-to-data covariance values and \(C(\mathbf{u}_{}- \mathbf{u}_{k})\) are the data-to-unknown (or the location where the estimate is needed) covariance values calculated from a variogram model fitted to the experimental variogram of the \(y\)-data.

Step 2

Calculate the mean \(\bar{y}_2(\mathbf{u}_{})\) and the variance \(\sigma_2^2(\mathbf{u}_{})\) for the unsampled location conditioning to the collocated secondary data \(\{x_j(\textbf{u}_{i}), \;j=1,\ldots,m,\; i=1,\ldots,N\}\) through the normal equations:

\[\begin{split} &\bar{y}_2(\mathbf{u}_{})= \sum_{j=1}^{m} \mu_j x_j(\mathbf{u}_{})\\ &\sigma_2^2(\mathbf{u}_{})= 1 - \sum_{j=1}^{m} \mu_j \rho_{jY}\\ &\sum_{j=1}^{m} \mu_j \rho_{jk}= \rho_{kY}, \;\; k=1,\ldots,m \end{split}\]

where \(\{x_j(\mathbf{u}_{}), j=1, \ldots,m\}\) are the secondary data at the unsampled location, \(\rho_{kY}\) is the cross-correlation between the primary and secondary data, and \(\rho_{jk}\) is the cross-correlation between the secondary data.

Step 3

The updated conditional mean \(\bar{y}_U\) and variance \(\sigma_U^2\) merging primary and secondary data through Bayesian Updating is given as follows (note that the unsampled location \(\mathbf{u}_{}\) is dropped from the notation):

\[\begin{split} &\bar{y}_U = \frac{\sigma_1^2\bar{y}_2+\sigma_2^2\bar{y}_1}{\sigma_1^2-\sigma_1^2\sigma_2^2+\sigma_2^2}\\ &\sigma_U^2= \cfrac{\sigma_1^2\sigma_2^2}{\sigma_1^2- \sigma_1^2\sigma_2^2+\sigma_2^2} \end{split}\]

Switching the order of the primary and secondary data will not change the result of Bayesian Updating.

Mathematical Derivation

Recall

Recall Bayes Theorem:

\[\label{bys} P(A|B)=\cfrac{P(A)P(B|A)}{P(B)}\]

In the context of geostatistics, \(B\) represents the available data and \(A\) represents the value at an unsampled location, which is also the variable of the equation. \(P(B)\) is constant; therefore, this equation is often simplified to \[P(A|B) \propto P(A)P(B|A)\] where \(P(B|A)\) is referred to as the likelihood, \(P(A)\) as the prior, and \(P(A|B)\) as the posterior. In the Bayesian Updating framework, we assume that the primary data source informs on the prior \(P(A)\) and the secondary data source informs on the likelihood \(P(B|A)\) (Besag, 1986; Doyen, Boer, & Pillet, 1996). Under this formalism, the conditional distribution given the primary and secondary data is expressed as:

\[\label{poster} f_{Y |(n),\mathbf{x}}(y)\propto f_{Y |(n)}(y)f_{\mathbf{x} | Y}(\mathbf{x}).\]

Before giving the expression of prior and likelihood, let’s examine the conditional mean and variance in a standard Gaussian space \(N(0,1)\). Consider a set of \(n \; (n=n_1 + n_2)\) multivariate Gaussian random variables. The conditional distribution of the first \(n_1\) random variables given \(n_2\) data values is multi-Gaussian with mean vector \(\boldsymbol{\mu}_{1|2}\) and covariance matrix \(\boldsymbol{\rho}_{1|2}\) calculated by the well known normal equation (Johnson & Wichern, 2002):

\[\label{gaeq} \begin{split} \boldsymbol{\mu_{1|2}}&=\boldsymbol{\rho}_{12} \boldsymbol{\rho}_{22}^{-1}\mathbf{x}_2 \\ \boldsymbol{\rho_{1|2}} &= \boldsymbol{\rho}_{11} - \boldsymbol{\rho}_{12} \boldsymbol{\rho}_{22}^{-1} \boldsymbol{\rho}_{21} \end{split}\]

where \(\mathbf{x}_2\) is the \(n_2\) dimension random variable values and the \(n\) dimension cross-correlation matrix has the form of \(\boldsymbol{\rho}= \begin{bmatrix} \boldsymbol{\rho}_{11} & \boldsymbol{\rho}_{12} \\ \boldsymbol{\rho}_{21} & \boldsymbol{\rho}_{22} \end{bmatrix}\).

Derivation of Bayesian Updating Equation

First, consider the prior. Since the primary variable \(Y\) is Gaussian, all conditional distributions have a Gaussian shape:

\[\label{prior} \begin{split} f_{Y |(n)}(y)&\propto \exp \left( -\frac{(y- \bar{y}_1)^2 }{2\sigma_1^2}\right)\\ &\propto \exp \left( -\frac{y^2}{2\sigma_1^2} + \frac{y \bar{y}_1}{\sigma_1^2}-\frac{\bar{y}_1^2}{2\sigma_1^2} \right) \\ &\propto \exp \left(-\frac{y^2}{2\sigma_1^2} + \frac{y \bar{y}_1}{\sigma_1^2}\right) \end{split}\]

where \(\bar{y}_1\) and \(\sigma_1^2\) are conditional mean and variance calculated from the normal equations given in Step 1:

\[\begin{split} \bar{y}_1&= \boldsymbol{\rho}_{0n} \boldsymbol{\rho}_{nn}^{-1} \mathbf{y} \\ \sigma_1^2&= 1 - \boldsymbol{\rho}_{0n} \boldsymbol{\rho}_{nn}^{-1} \boldsymbol{\rho}_{n0}, \end{split}\]

where \(\boldsymbol{\rho}_{0n}\) is the spatial correlation between \(y\) and \(n\) available primary data, \(\mathbf{y}\) is the available primary data, and \(\boldsymbol{\rho}_{nn}\) is the spatial correlation between the available primary data in the domain, both of which are calculated from the analytical model fitted to the experimental variogram of the primary data.

Now, consider the likelihood (based on the collocated secondary data). Since all variables are multivariate Gaussian distributed, the conditional likelihood also has a Gaussian shape,

\[\label{liki} f_{\mathbf{x} | Y}(\mathbf{x})\propto \exp \left(-\frac{1}{2} [\mathbf{x}-\mathbf{b}_x]^T \mathbf{\rho}_x^{-1} [\mathbf{x}-\mathbf{b}_x]\right),\]

where \(\mathbf{b}_x\) is the conditional mean of \(\mathbf{x}\) given \(y\) and \(\mathbf{\rho}_x^{-1}\) is the conditional covariance matrix with the dimension of \(m \times m\). The likelihood is the probability distribution of the secondary data \(\mathbf{x}\) given \(y\), while the prior is the probability distribution of \(y\) given the sampled primary data \((n)\).

From the normal equations,

\[\label{spm} \begin{split} \mathbf{b}_x= \boldsymbol{\rho}_{0m} y \\ \boldsymbol{\rho}_x= \boldsymbol{\rho}_{mm}- \boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T \end{split}\] where \[\boldsymbol{\rho}_{mm}= \begin{pmatrix} \rho_{11} & \ldots & \rho_{1m} \\ \vdots & \ddots & \vdots \\ \rho_{m1} & \ldots & \rho_{mm} \end{pmatrix} \;\;\boldsymbol{\rho}_{0m}=[\rho_{10}, \ldots, \rho_{m0}]^T\]

The likelihood with the mean and the variance:

\[\label{pf} \begin{split} f_{\mathbf{x} | Y}(\mathbf{x})&\propto \exp ( -\frac{1}{2} \left[\mathbf{x} -\boldsymbol{\rho}_{0m}y\right]^T \boldsymbol{\rho}_x^{-1} [\mathbf{x}-\boldsymbol{\rho}_{0m}y]) \\ &\propto \exp ( -\frac{1}{2} [ \mathbf{x}^T -\boldsymbol{\rho}_{0m}^T y]\boldsymbol{\rho}_x^{-1} [\mathbf{x}-\boldsymbol{\rho}_{0m}y]) \\ &\propto \exp ( -\frac{1}{2}[\mathbf{x}^T \boldsymbol{\rho}_x^{-1} \mathbf{x} -2 \boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_x^{-1} \mathbf{x} y + \boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_x^{-1} \boldsymbol{\rho}_{0m}y^2) \end{split}\]

Since \(\mathbf{x}\) is fixed and \(y\) is the variable, after eliminating the proportionality constant, this equation is simplified to

\[\label{finf} f_{\mathbf{x} | Y}(\mathbf{x})\propto \exp \left(-\frac{\boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_x^{-1} \boldsymbol{\rho}_{0m}}{2} \cdot y^2 + \boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_x^{-1} \mathbf{x} y \right).\]

The next step is to simplify the likelihood equation into a more concise format which shares a similar form with the prior results (Ren, 2007). The conditional mean (\(\bar{y}_2\)) and the variance (\(\sigma^2_2\)) of \(y\) given \(\mathbf{x}\) are to be used to represent the coefficients of the polynomial terms in the likelihood results. First, let’s rewrite the equations for \(\bar{y}_2\) and \(\sigma^2_2\), which also come from the normal equations given in Step 2:

\[\label{kp} \begin{split} &\bar{y}_2 = \sum_{i=1}^{m} \lambda_i x_i \\ &\sigma_2^2= 1 - \sum_{i=1}^{m} \lambda_i \rho_{jy} \\ &\sum_{i=1}^{m} \lambda_i \rho_{i,k} = \rho_{k,0}, \;\; k=1,\ldots,m \end{split}\]

In a matrix form, \(\mathbf{\lambda}^T=\boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_{mm}^{-1}\), the mean and covariance are expressed as:

\[\begin{split} \bar{y}_2=\boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_{mm}^{-1} \mathbf{x} \\ \sigma_2^2 =1 - \boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m} \end{split}\]

Then, the expression of \(\boldsymbol{\rho}_x^{-1}\) is developed. From the previous section:

\[\label{revx} \begin{split} \boldsymbol{\rho}_x&= \boldsymbol{\rho}_{mm}-\boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T \\ &= \boldsymbol{\rho}_{mm}(1- \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T)\\ \boldsymbol{\rho}_x^{-1}&= (1- \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T)^{-1} \boldsymbol{\rho}_{mm}^{-1} \end{split}\] The coefficient of the linear term \(\boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_x^{-1} \mathbf{x}\) are expressed as: \[\label{b1} \begin{split} \boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_x^{-1} \mathbf{x} &= \boldsymbol{\rho}_{0m}^T (1- \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T)^{-1} \boldsymbol{\rho}_{mm}^{-1} \mathbf{x} \\ &=\boldsymbol{\rho}_{0m}^T (1- \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T)^{-1}\boldsymbol{\rho}_{0m}^{T^{-1}} \boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_{mm}^{-1}\mathbf{x} \\ &=\boldsymbol{\rho}_{0m}^T (\boldsymbol{\rho}_{0m}^T- \boldsymbol{\rho}_{0m}^T\boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T)^{-1} \bar{y}_2\\ &=\boldsymbol{\rho}_{0m}^T (\boldsymbol{\rho}_{0m}^T- (1-\sigma_2^2)\boldsymbol{\rho}_{0m}^T)^{-1}\bar{y}_2\\ &=\boldsymbol{\rho}_{0m}^T(\sigma_2^2\boldsymbol{\rho}_{0m}^T)^{-1} \bar{y}_2\\ &=\frac{\bar{y}_2}{\sigma_2^2} \end{split}\]

The same method is applied to the quadratic term coefficient \(\boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_x^{-1} \boldsymbol{\rho}_{0m}\):

\[\label{b2} \begin{split} \boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_x^{-1} \boldsymbol{\rho}_{0m}&= \boldsymbol{\rho}_{0m}^T (1- \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T)^{-1} \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\\ &=\boldsymbol{\rho}_{0m}^T (1- \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T)^{-1} \boldsymbol{\rho}_{0m}^{T^{-1}} \boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\\ &=\boldsymbol{\rho}_{0m}^T (\boldsymbol{\rho}_{0m}^T- \boldsymbol{\rho}_{0m}^T \boldsymbol{\rho}_{mm}^{-1} \boldsymbol{\rho}_{0m}\boldsymbol{\rho}_{0m}^T)^{-1}(1-\sigma_2^2) \\ &=\boldsymbol{\rho}_{0m}^T (\boldsymbol{\rho}_{0m}^T - (1-\sigma_2^2)\boldsymbol{\rho}_{0m}^T)^{-1} (1- \sigma_2^2) \\ &= \boldsymbol{\rho}_{0m}^T (\sigma_2^2\boldsymbol{\rho}_{0m}^T)^{-1} (1-\sigma_2^2) \\ &=\frac{1-\sigma_2^2}{\sigma_2^2} \end{split}\]

Now substituting the two coefficients back into the likelihood gives a simplified form of the likelihood:

\[\label{cc} f_{\mathbf{x} | Y}(\mathbf{x})\propto \exp\left(-\frac{1-\sigma_2^2}{2 \sigma_2^2} y^2 + \frac{\bar{y}_2}{\sigma_2^2} y \right)\]

Substituting the prior and the likelihood back to the posterior equation gives the form of the combined probability distribution of \(y\) given the primary and secondary data:

\[\label{postfin} \begin{split} f_{Y |(n), \mathbf{x}}(y)\propto \exp \left(-\frac{1}{2}\left[ \frac{1-\sigma_2^2}{\sigma_2^2} +\frac{1}{\sigma^2_1}\right] y^2+ \left[\frac{\bar{y}_2}{\sigma_2^2} +\frac{\bar{y}_1}{\sigma_1^2}\right] y \right) \end{split}.\]

This has the form of \(\exp(-Ax^2+Bx)\) which can be rearranged to a standard Gaussian distribution form with the updated conditional mean and variance:

\[\label{conleq} \begin{split} &\bar{y}_U = \frac{B}{2A}=\cfrac{\cfrac{\bar{y}_2}{\sigma_2^2} + \cfrac{\bar{y}_1}{\sigma_1^2}}{\cfrac{1-\sigma_2^2}{\sigma_2^2}+\cfrac{1}{\sigma_1^2}}= \frac{\sigma_1^2\bar{y}_2+\sigma_2^2\bar{y}_1}{\sigma_1^2-\sigma_1^2\sigma_2^2+\sigma_2^2}\\ &\sigma_U^2=\frac{1}{2A}=\cfrac{1}{\cfrac{1-\sigma_2^2}{\sigma_2^2}+\cfrac{1}{\sigma_1^2}}= \cfrac{\sigma_1^2\sigma_2^2}{\sigma_1^2- \sigma_1^2\sigma_2^2+\sigma_2^2} \end{split},\]

These are the equations for Bayesian Updating.

In the final posterior equation given above, the \(\exp(-Ax^2+Bx)\) form gives the value of updated mean and variance. When estimating the probability distribution, there is only one variable \(y\), so consider a standard univariate Gaussian distribution:

\[\label{a2} \begin{aligned} g(m,\sigma) &\propto \exp ( -\cfrac{1}{2}[x- m]^T \sigma^{2^{-1}} [x- m]) \\ & \propto \exp\left(-\cfrac{x^2-2mx+m^2}{2\sigma^2} \right) \\ & \propto \exp\left(-\cfrac{1}{2\sigma^2}\cdot x^2 + \cfrac{m}{\sigma^2} \cdot x \right) \end{aligned}\]

In this equation, suppose \(\cfrac{1}{2\sigma^2}= A\) and \(\cfrac{m}{\sigma^2}=B\). It is easy to prove that \(\sigma^2= \cfrac{1}{2A}\) and \(m=\cfrac{B}{2A}\), which are the updated mean and variance.

Summary

Bayesian Updating is a robust method that combines the information from primary and multiple secondary variables in order to generate a posterior (or updated) conditional probability distribution of the primary variable to be predicted \(f_{Y |(n),\mathbf{x}}(y)\). At each grid node, the posterior distribution is obtained as a product of the conditional distribution of all secondary variables given the primary variable to be predicted \(f_{\mathbf{x} | Y}(\mathbf{x})\) and the conditional distribution of the primary variable to be predicted given available primary data \(f_{Y |(n)}(y)\). Considering the Bayesian inference, the former conditional distribution accounts for the influence of the secondary information and the latter conditional distribution accounts for the influence of the primary variable. The major assumption in Bayesian Updating is that the conditional distribution of all secondary variables given the primary variable is obtained by considering only the collocated available secondary variables with the primary variable to be predicted, which is in fact identical to Markov-type screening hypothesis in collocated cokriging.

The simplicity of Bayesian Updating lies in the fact that the Bayesian Updating process does not require the spatial cross-correlation between primary and secondary data, which is a necessity in collocated cokriging. In the cokriging context, all available data (primary and secondary) are combined in one Gaussian space, and to describe this space, the correlation between dimensions are required. If this space can be described parametrically, the conditional distribution (mean and variance) at the unsampled location (one dimension in the space) can be viewed as other data dimensions’ projection at that dimension. This is why normal equations are used when calculating conditional distributions. However, it is difficult to parameterize this large Gaussian space, therefore, Bayesian Updating is adopted as a way to combine two Gaussian spaces (primary and secondary data space) together, and the combination is based on Bayes Theorem. The two separate Gaussian spaces are easy to describe. The primary data space is defined by the variogram. The secondary data space is parameterized by the correlations calculated from the data. The collocated assumption avoids the spatial correlation requirement in the secondary space. Thus, the variance map for the secondary data is constant in the domain.

The interpretation of prior or likelihood does not influence the final updated results, which can be observed in the Bayesian Updating equations. Each data source provides a conditional mean and variance of \(y\). Despite the format and derivation difference in Bayesian Updating and collocated cokriging under the Markov-type screening hypothesis, these two methods produce identical results. In the presence of multiple secondary variables, Bayesian Updating may be advantageous because there is no need for the linear coregionalization model to be fitted for all available variables, which is a requirement of the conventional geostatistical algorithms. When multiple secondary variables are available, As with the other geostatistical prediction algorithms, Bayesian Updating also produces the estimation variance indicating the uncertainty associated with the estimate assigned to the particular location.

References